当计算撞上内存墙：Attention！注意力机制及其优化算法浅析

2023 年 11 月，英伟达又一次发布了 H200¹，号称性能飙升 90%，LLaMA 2 推理速度翻倍。事实上，如果你仔细对比 H200 SXM 和 H100 SXM 的 Specification，你就会发现本次 H200 发布只是提升了 GPU 内存容量和带宽，并从 HBM3 升级成了 HBM3e，而算力单元并没有改变。或许是为了应对 AMD 在今年 6 月发布的 192GB HBM3 显存 5.2 TB/s 带宽的 MI300X 芯片²，在发布 Hopper 架构之后，从年初的 3 月到年底的 11 月，这已经是老黄在今年第 4 次基于 Hopper 架构对 GPU 内存动心思并对外做产品发布了³⁴⁵⁶。

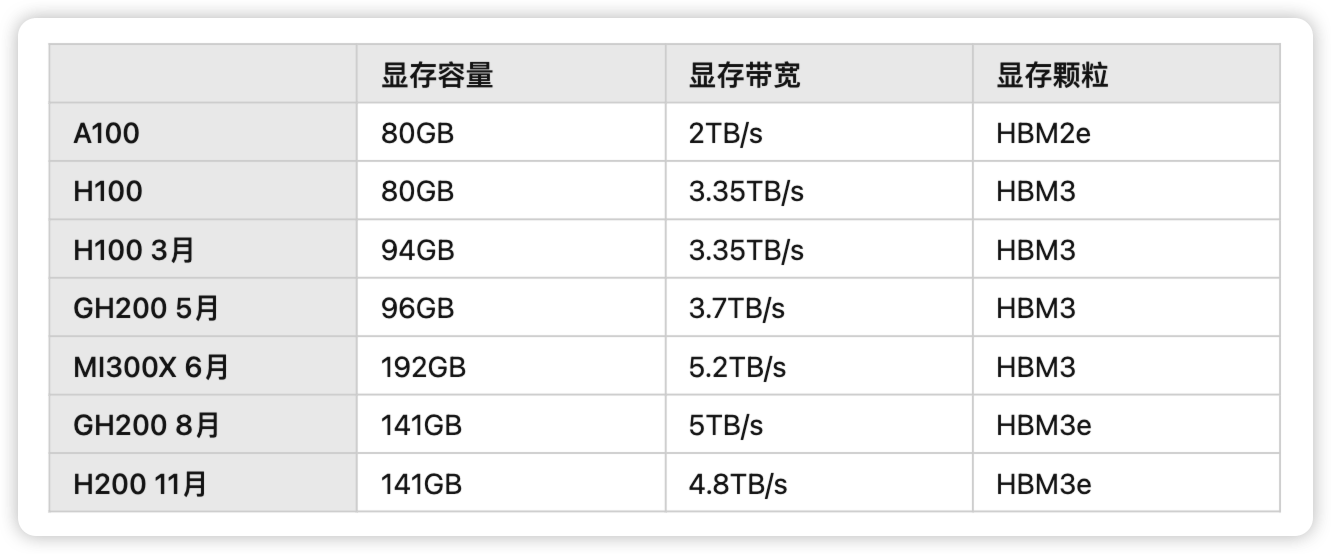
在大语言模型迅速发展的当下，为什么 GPU 内存会如此重要，让老黄在 Hopper 架构上一年内反复升级内存容量和带宽？本文尝试从 2017 年的那篇 Attention Is All You Need⁷ 论文出发，通过对 Attention 机制的理解，从算法的角度去分析当前深度学习系统中 Attention 对于内存容量和带宽的需求。通过介绍以 FlashAttention⁸ 和 PagedAttention⁹ 为代表的对标准 Attention 的各种优化算法，理解内存对于大语言模型的上下文长度的增长的限制。

TLDR

• 本文所有的资料来自于互联网公开信息，更多是从程序员的角度去理解 Attention 及其算法原理，推荐大家阅读本文附录的原始资料，文中的观点与本人雇主无关。
• 作为一名软件工程师，本文作者对于算法的理解也并不算深刻与全面，甚至可能会存在偏差与错误，在介绍相关方向的时候也肯定会存在遗漏，欢迎大家交流与指正。
• 在推理优化的介绍中，本文仅仅简单介绍了 KV Cache 和 PagedAttention，对于蒸馏、量化、稀疏和窗口优化等其他常见的优化方法都没有介绍，可以参考这篇文章¹⁰。
• 本文相对较长，全文超过一万字，并且包含较多数学公式与图片，Attention！建议关注、收藏后观看，也可访问我的博客获得更好阅读体验  https://loop.houmin.site/context/attention 。

Memory Wall

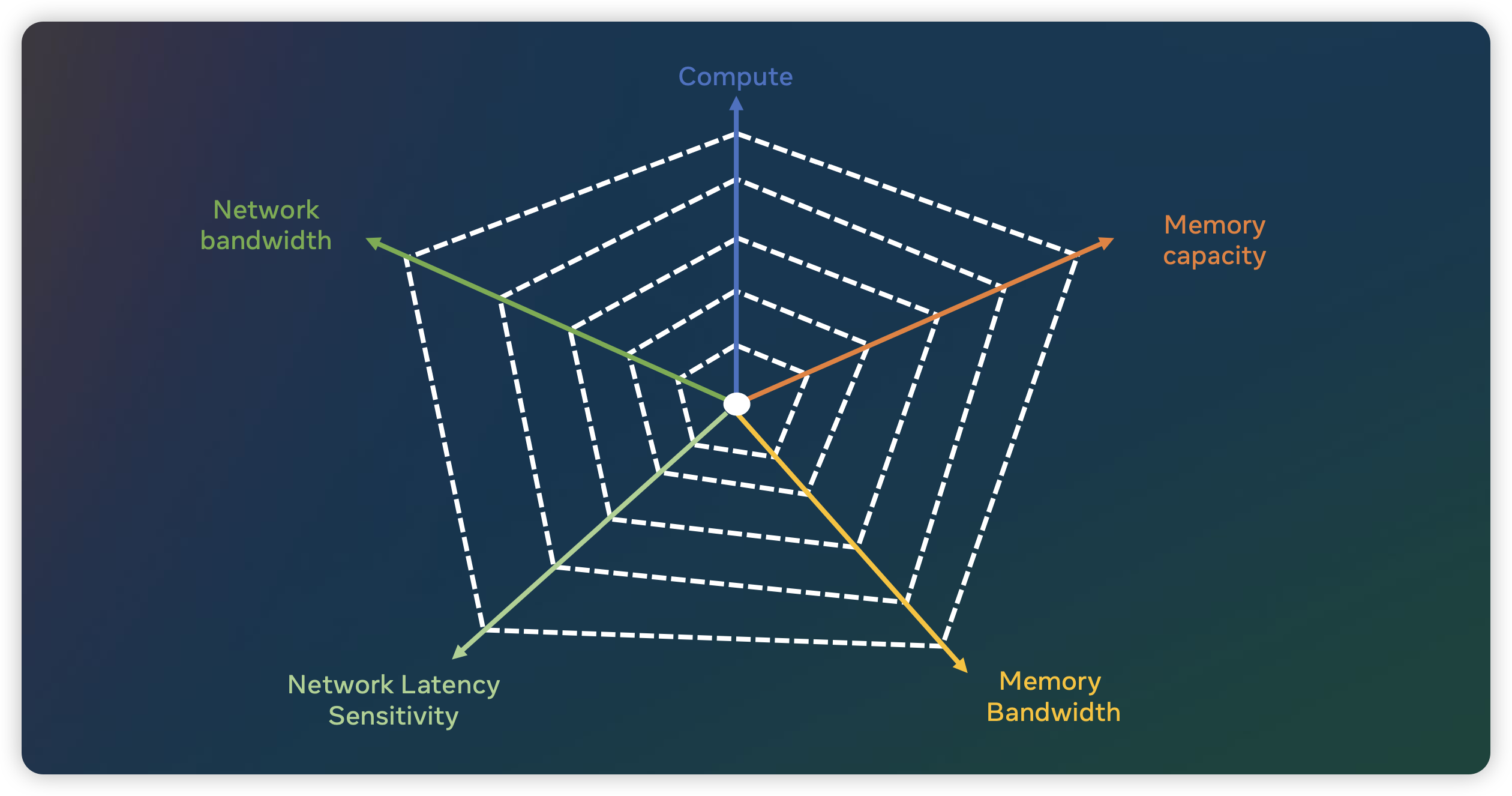
在上一篇文章 疯狂的 H100：现代 GPU 体系结构浅析，从算力焦虑开始聊起 中我们初步介绍了当前大模型对于算力的巨大需求。然而，对于一个机器学习系统来说，算力并不是其考虑的唯一因素，内存与网络在系统设计中也占据着重要地位。在了解过算力需求之后，本文讲重点讨论模型训练和推理中对于内存的需求，关于网络的讨论之后有机会再写一篇。

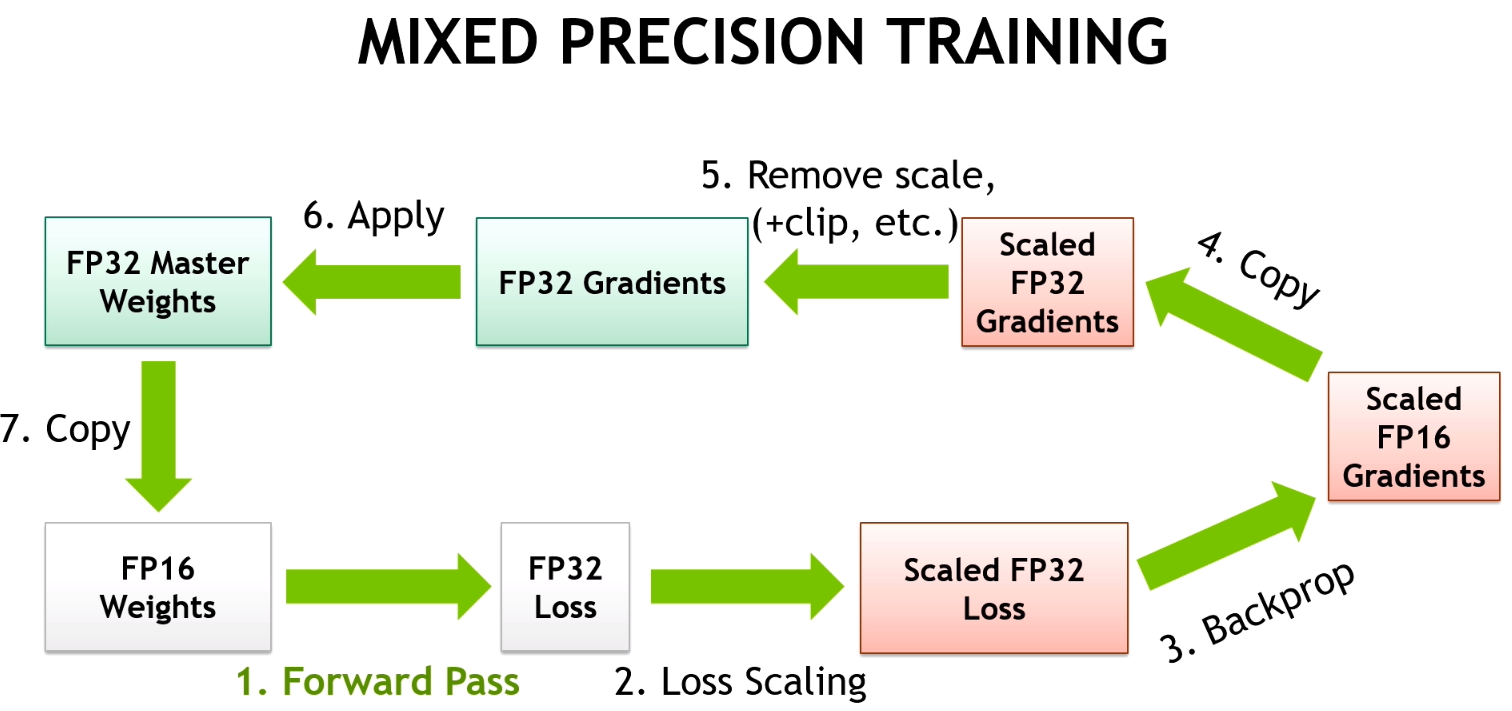
论文 ZeRO: Memory Optimizations Toward Training Trillion Parameter Models¹¹ 详细分析了在训练中所有 GPU 内存消耗的占比。现在基于 NVIDIA GPU 训练大模型的常见范式是混合精度 (fp16/fp32) 训练¹²：

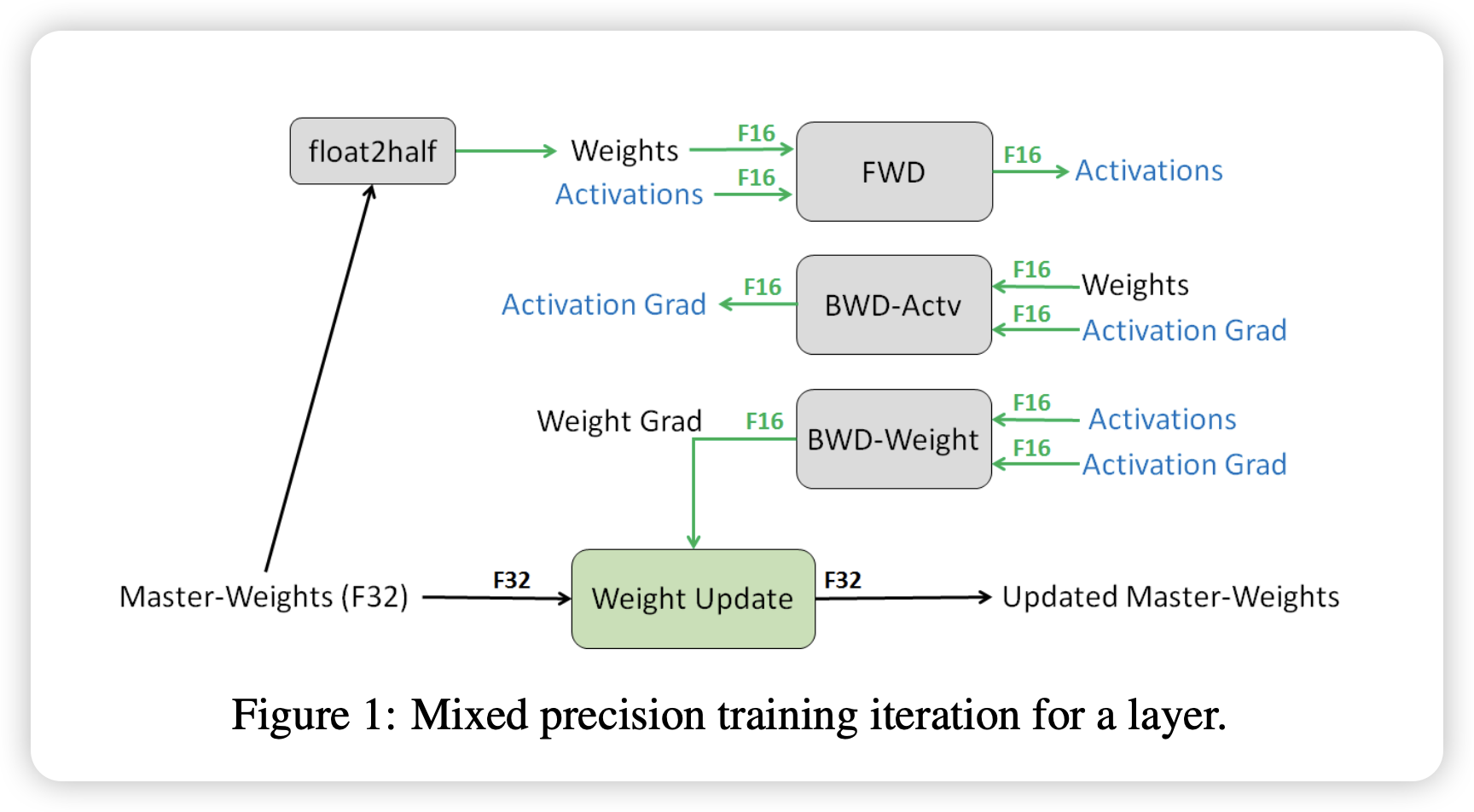
1. Maintain a primary copy of weights in FP32.¹³
2. Initialize S to a large value.
3. For each iteration:
   1. Make an FP16 copy of the weights.
   2. Forward propagation (FP16 weights and activations).
   3. Multiply the resulting loss with the scaling factor S.
   4. Backward propagation (FP16 weights, activations, and their gradients).
   5. If there is an Inf or NaN in weight gradients:
      1. Reduce S.
      2. Skip the weight update and move to the next iteration.
   6. Multiply the weight gradient with 1/S.
   7. Complete the weight update (including gradient clipping, etc.).
   8. If there hasn’t been an Inf or NaN in the last N iterations, increase S

在梯度更新中，目前应用最为广泛的是 Adam 优化算法，需要引入梯度的一阶动量和二阶动量，计算方法如下图所示：

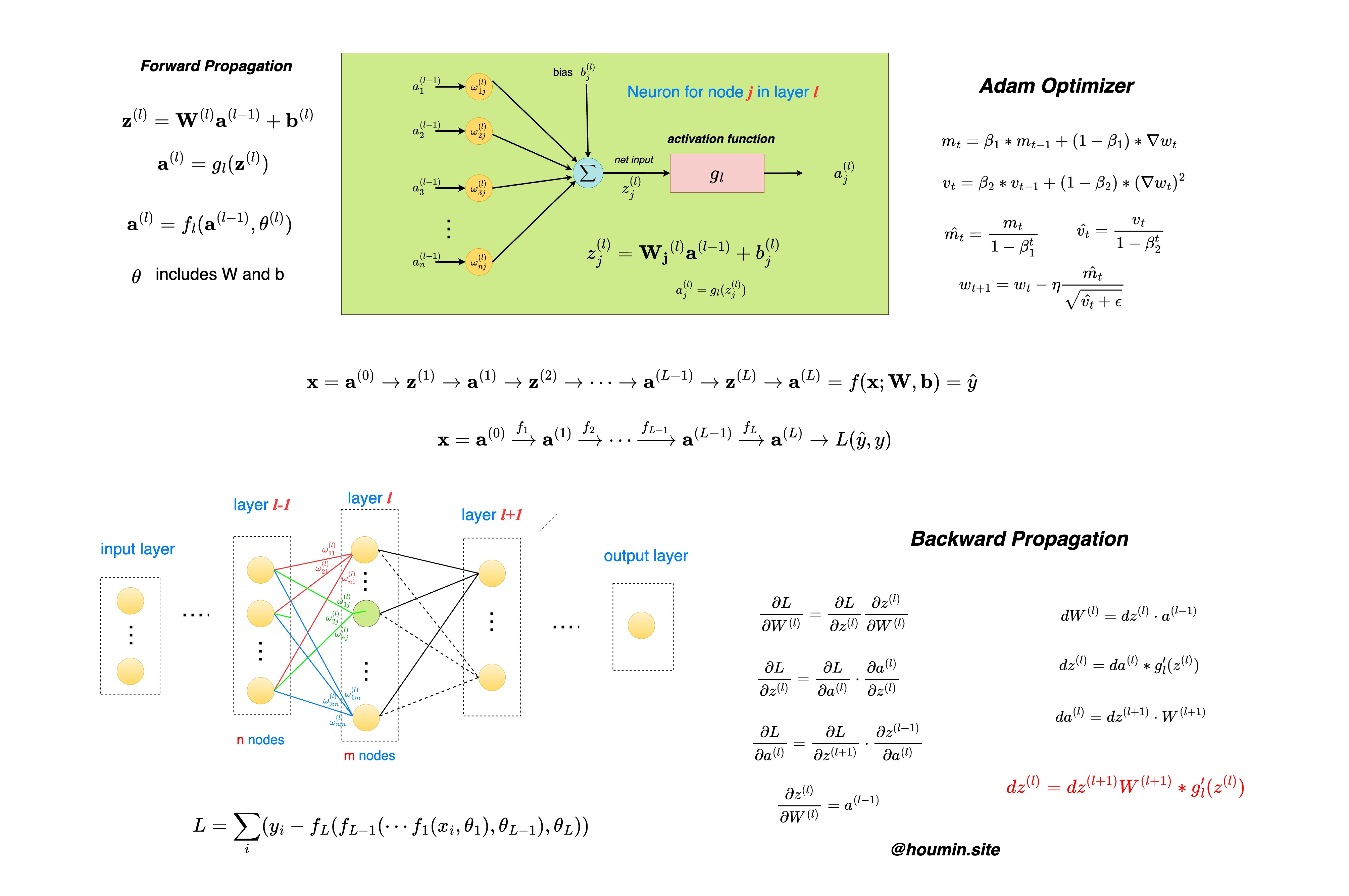
因此，使用了 Adam 优化器的混合精度训练中，内存消耗占比如下：

• Weights：模型参数，每个 fp16 参数占据 2 个字节，混合精度训练时对每个 fp16 参数还会保存一个 fp32 的模型参数
• Activations：前向计算过程中产生的中间激活，这部分内存占用比较大，通常可以通过 Activation Checkpointing 来优化，这里暂时不算这部分
• Gradients：反向传递计算得到的梯度，用 fp16 表示
  • 在 ZeRO-Infinity¹⁴ 补充到还需要保存 fp32 的梯度，如果 Optimizer 做了 fuse 的话，fp32 的梯度也不需要了
• Optimizer States：优化器状态
  • 历史梯度的滑动平均，即一阶动量 momentum，用 fp32 表示
  • 历史梯度平方的滑动平均，即二阶动量 variance，用 fp32 表示

总结一下，对于 Adam 优化器的混合精度训练，每个参数需要 weights(fp16+fp32) + gradients(fp16+fp32) + optimizer states(fp32+fp32) 的内存空间，也就是一个参数对应 20 个字节的内存占用：

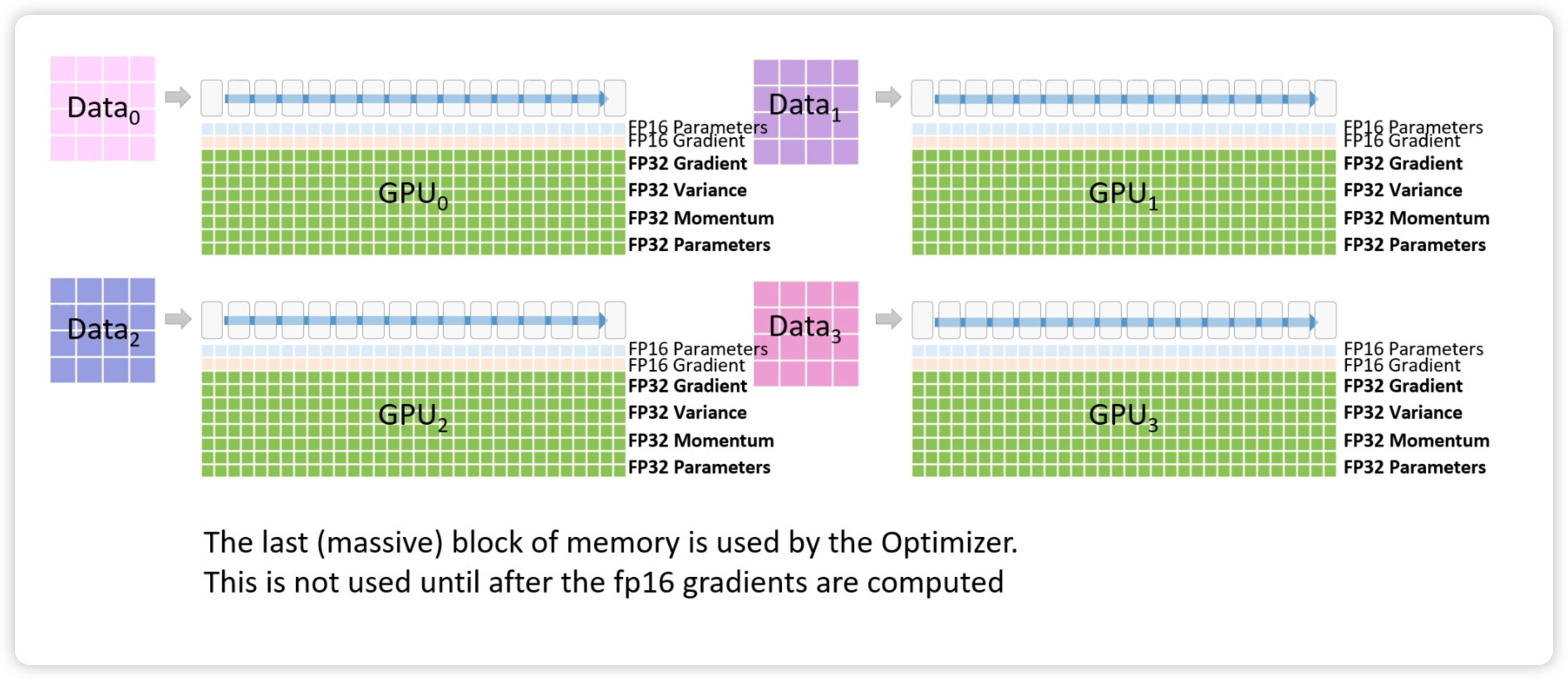
对于 GPT-3 175B 的参数，按照这个方法计算，在训练中总共需要的内存消耗为 175 * 20 GB = 3500GB，显然已经远远超出了目前主流 GPU 的内存容量。

Transformer

上面我们基于通用的神经网络架构来计算，直观地感受了下目前大语言模型对于 GPU 内存容量的需求。接下来，我们将结合 Andrej Karpathy 的 nanoGPT¹⁴ 项目，基于以 GPT 为代表的 decoder-only 的 Transformer 架构来计算其对于算力和内存的需求，从数字上获得更加明确的感受。

本节采用的数学符号表示如下

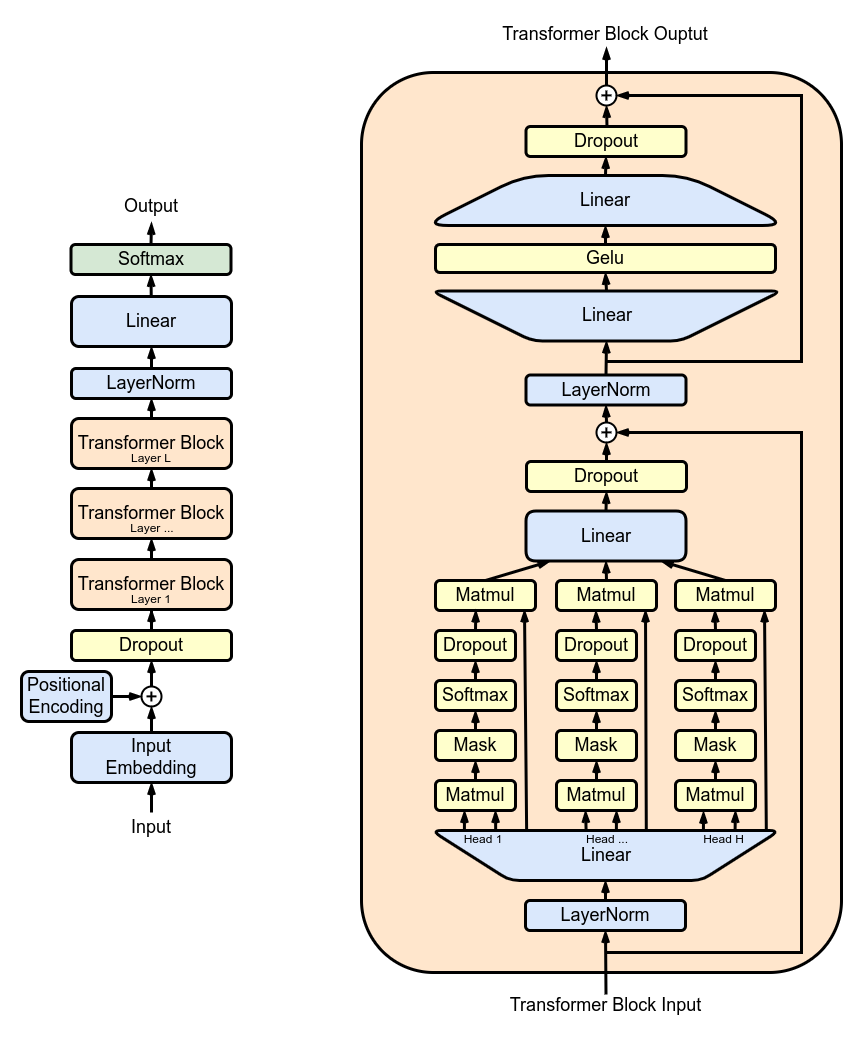
上图是典型的以 GPT 为代表的 decoder-only Transformer 架构，对应到代码表示，我们可以直接计算在模型结构的各个参数的维度：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class GPT(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config

        self.transformer = nn.ModuleDict(dict(
            wte = nn.Embedding(config.vocab_size, config.n_embd),
            wpe = nn.Embedding(config.block_size, config.n_embd),
            drop = nn.Dropout(config.dropout),
            h = nn.ModuleList([Block(config) for _ in range(config.n_layer)]),
            ln_f = LayerNorm(config.n_embd, bias=config.bias),
        ))
        self.lm_head = nn.Linear(config.n_embd, config.vocab_size, bias=False)
        self.transformer.wte.weight = self.lm_head.weight

解释一下这里 Config 配置的主要参数

• vocab_size 是词表大小，对应于在 Math Notation 中的 $V$
• n_embd 是 embedding size，也就是表示 token 的向量的维度
  • 一般也等于隐藏层的维度，也就是 hidden size，对应于在 Math Notation 中的 $C$
  • 如果 embedding size 和 hidden size 不一样，模型结构中需要加上对应的 projection layer
• n_head 指的是 multi-head attention 里面 head 的数目，对应于在 Math Notation 中的 $n_{head}$
• n_layer 指的是 transformer block 的数目，在 Math Notation 中的 $l$
• block_size 指的是 input sequence 的最大长度，也就是 input sequence 中 tokens 的数目，对应于在 Math Notation 中的 $T$

下面是 nanoGPT 中的一个典型的配置：

1
2
3
4
5
6
7
8
9

@dataclass
class GPTConfig:
    block_size: int = 1024
    vocab_size: int = 50304 # GPT-2 vocab_size of 50257, padded up to nearest multiple of 64 for efficiency
    n_layer: int = 12
    n_head: int = 12
    n_embd: int = 768
    dropout: float = 0.0
    bias: bool = True # True: bias in Linears and LayerNorms, like GPT-2. False: a bit better and faster

Embeddings

在 tokenization 的过程中我们需要将搜集到的语料转化成对应的 token embedding 向量¹⁵，常见的算法包括 BPE、WordPiece、Unigram 和 SentencePiece 等。

以 GPT-2 使用的 BytePair Encoding 算法¹⁶为例，词表大小为 50257，也即是对应着  256  个  byte-base token 、一个特殊的文本结束  token 、以及通过  50000  次  merge  所学到的  symbol ，这也是为什么训练的时候需要有 vacab file 和 merge table 两个文件。

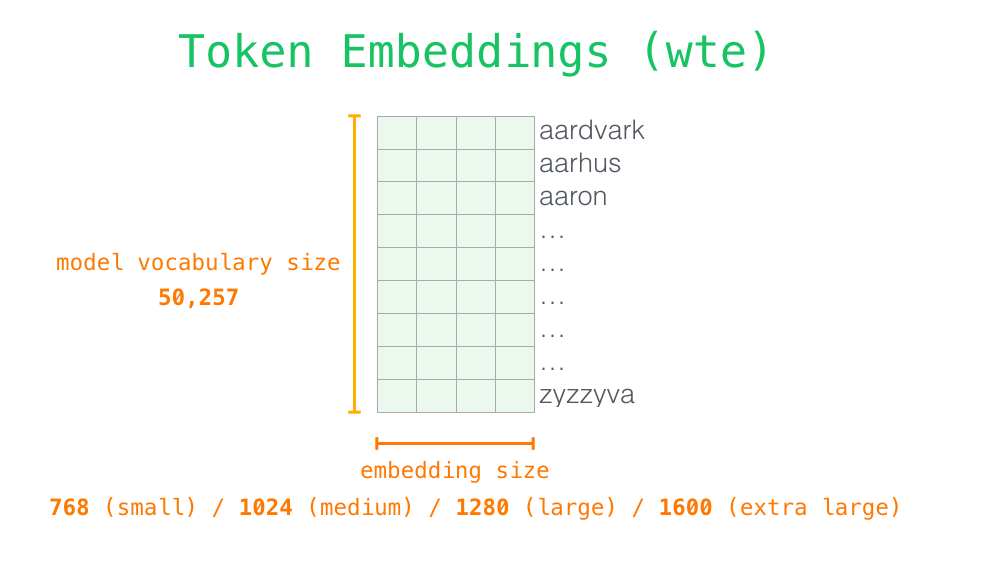
在模型输出的时候，我们可以选择 Vocab 表中和其最近的 token 作为字符串输出。

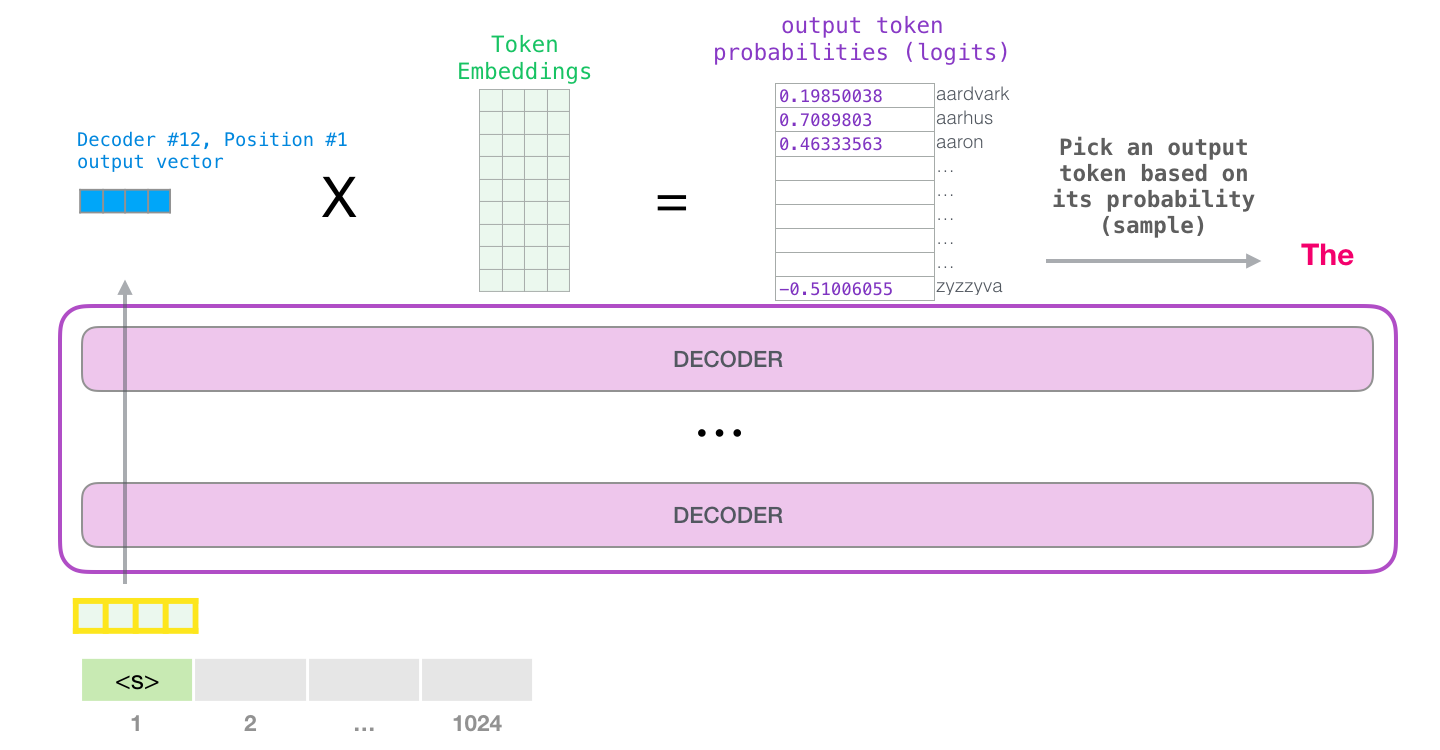
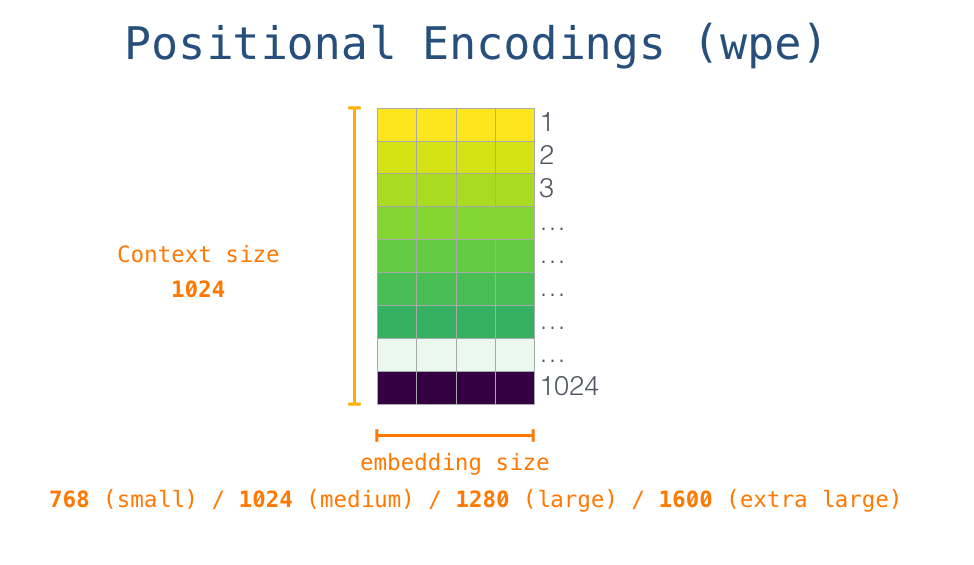
为了体现出同一个 sequence 中不同 token 的位置含义，一般会在 wte 加上加权位置编码 wpe。wpe 矩阵的宽度为 embedding size，长度则是 context size，也就是前面说的 sequence length。

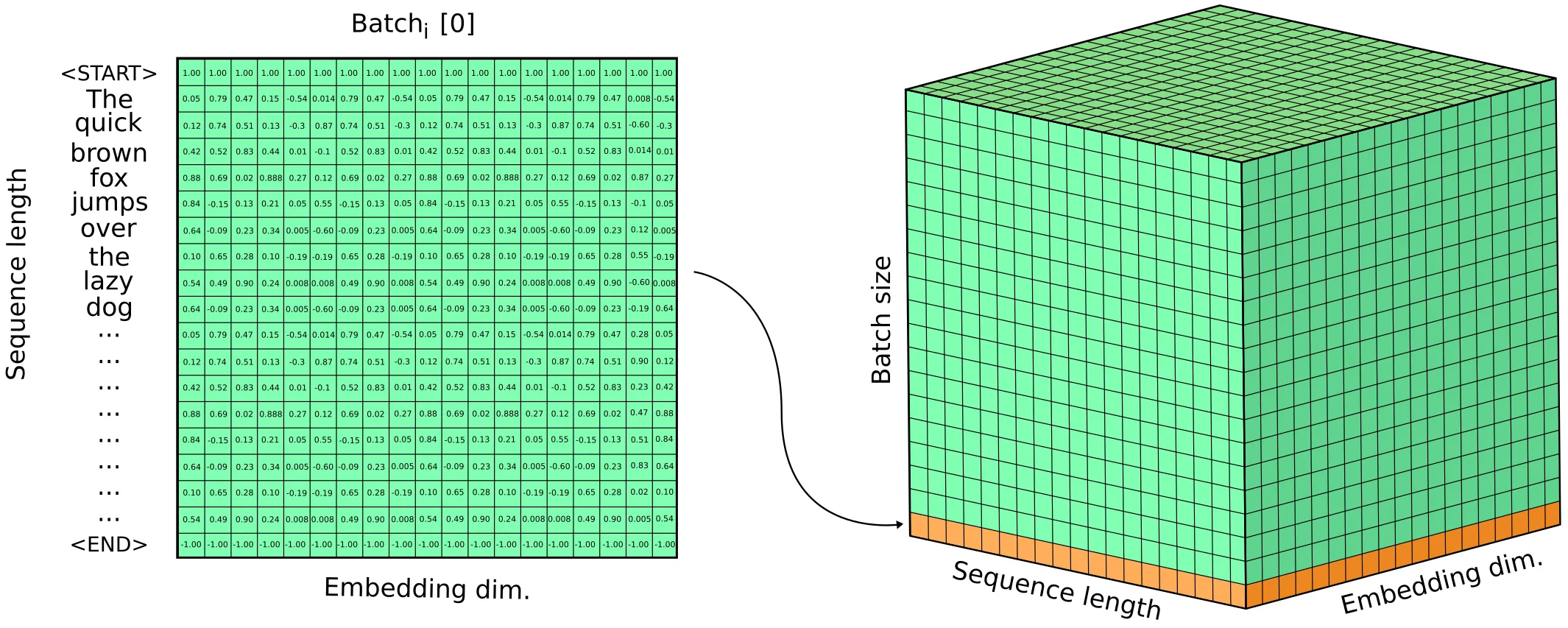
一般来说，训练时候会将一批 batch size 大小的 sequence 一起输入，因此输入 tensor 的维度为 (batch size, sequence length, embedding size)

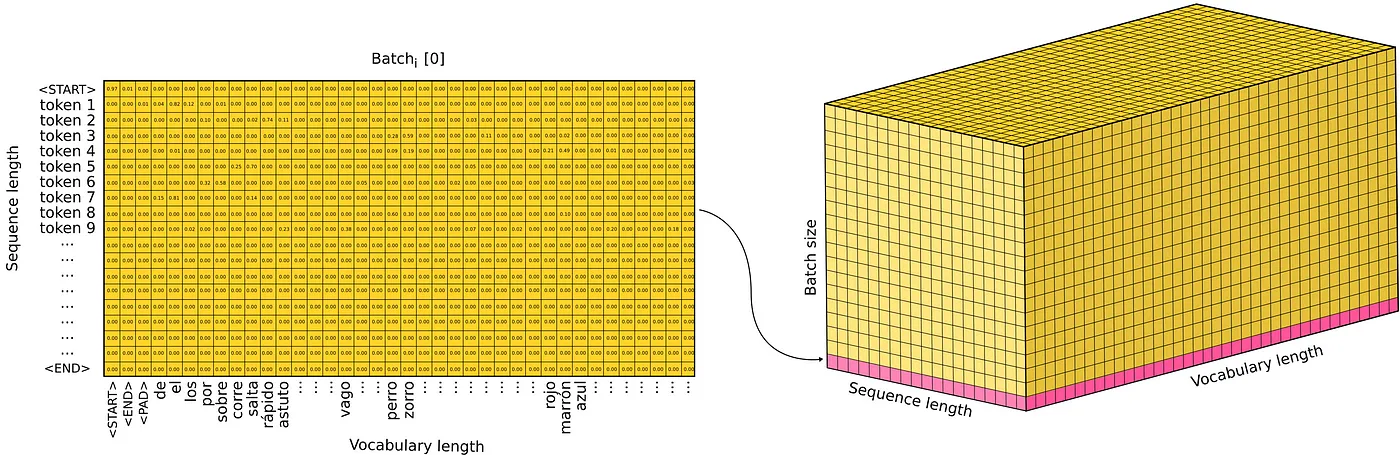
经过 Linear+Softmax 之后，输出 tensor 是一个 Output Probabilities，维度为 (batch size, sequence length, vocab size)

总结一下，GPT 代表的前向流程如下代码所示，十分清晰了：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

    def forward(self, idx, targets=None):
        device = idx.device
        b, t = idx.size()
        assert t <= self.config.block_size, f"Cannot forward sequence of length {t}, block size is only {self.config.block_size}"
        pos = torch.arange(0, t, dtype=torch.long, device=device) # shape (t)

        # forward the GPT model itself
        tok_emb = self.transformer.wte(idx) # token embeddings of shape (b, t, n_embd)
        pos_emb = self.transformer.wpe(pos) # position embeddings of shape (t, n_embd)
        x = self.transformer.drop(tok_emb + pos_emb) # input for dropout of shape (b, t, n_embd)
        for block in self.transformer.h:
            x = block(x)
            x = self.transformer.ln_f(x)
        logits = self.lm_head(x)
	# ...

Decoder Blocks

看完 Transformer 整体架构之后，进一步的，我们进入到最核心的 Transformer Layer，看看每一层的具体组成。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

class Block(nn.Module):

    def __init__(self, config):
        super().__init__()
        self.ln_1 = LayerNorm(config.n_embd, bias=config.bias)
        self.attn = CausalSelfAttention(config)
        self.ln_2 = LayerNorm(config.n_embd, bias=config.bias)
        self.mlp = MLP(config)

    def forward(self, x):
        x = x + self.attn(self.ln_1(x))
        x = x + self.mlp(self.ln_2(x))
        return x

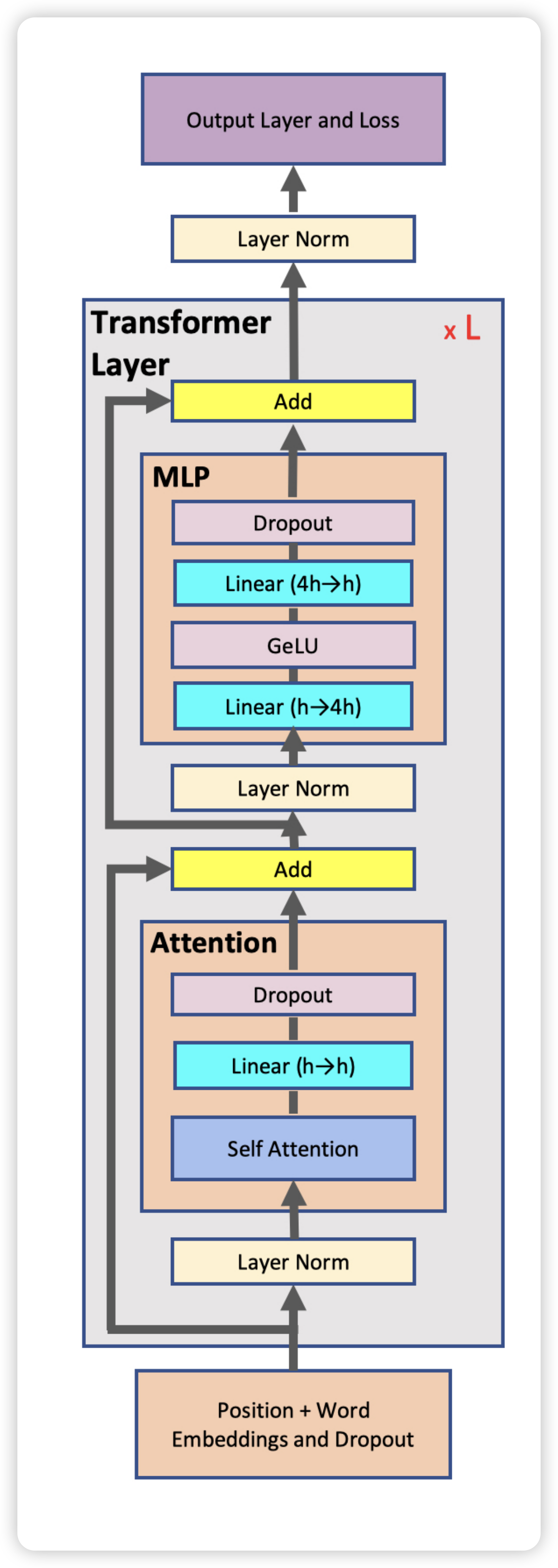
Attention Layer

Attention 机制可以捕捉到一个 sequence 之中各个 token 的相关性，相对于 RNN 的串行计算，Attention 机制天然可以并行，同时算出一个 sequence 中各个 token 之间所有的相关性。

$$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_{k}}}) V$$

如下图所示，为了计算出 token 之间的相关性，对于每一个 token，需要计算三个向量 query，key 和 value：

• 每个 token 需要通过自己的 query 和其他 token 的 key 计算，目前使用较多的是 dot-product 方式，来获得其他 token 在本 token 看到的 attention score。
• 以下图为例，token a1 在 token a2 眼中获得的 attention score 就是图中的 $\alpha^{\prime}_{2,1}$，这个 attention score 已经经过了 softmax 进行 normalization
• 网络的输出值 b2 需要将各个 token 在 token a2 获得的 attention score 结合自身的 value，加权求和得到

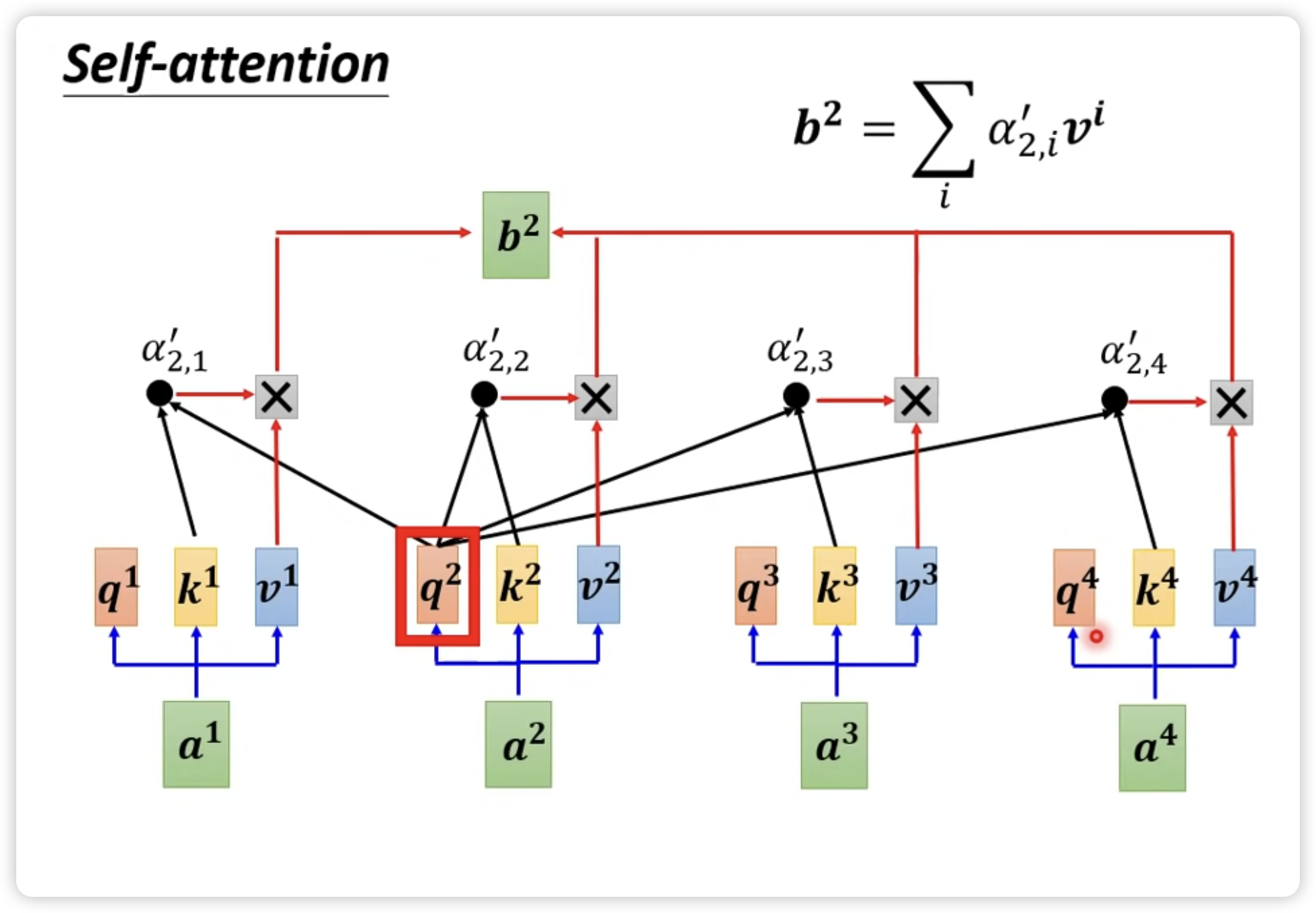
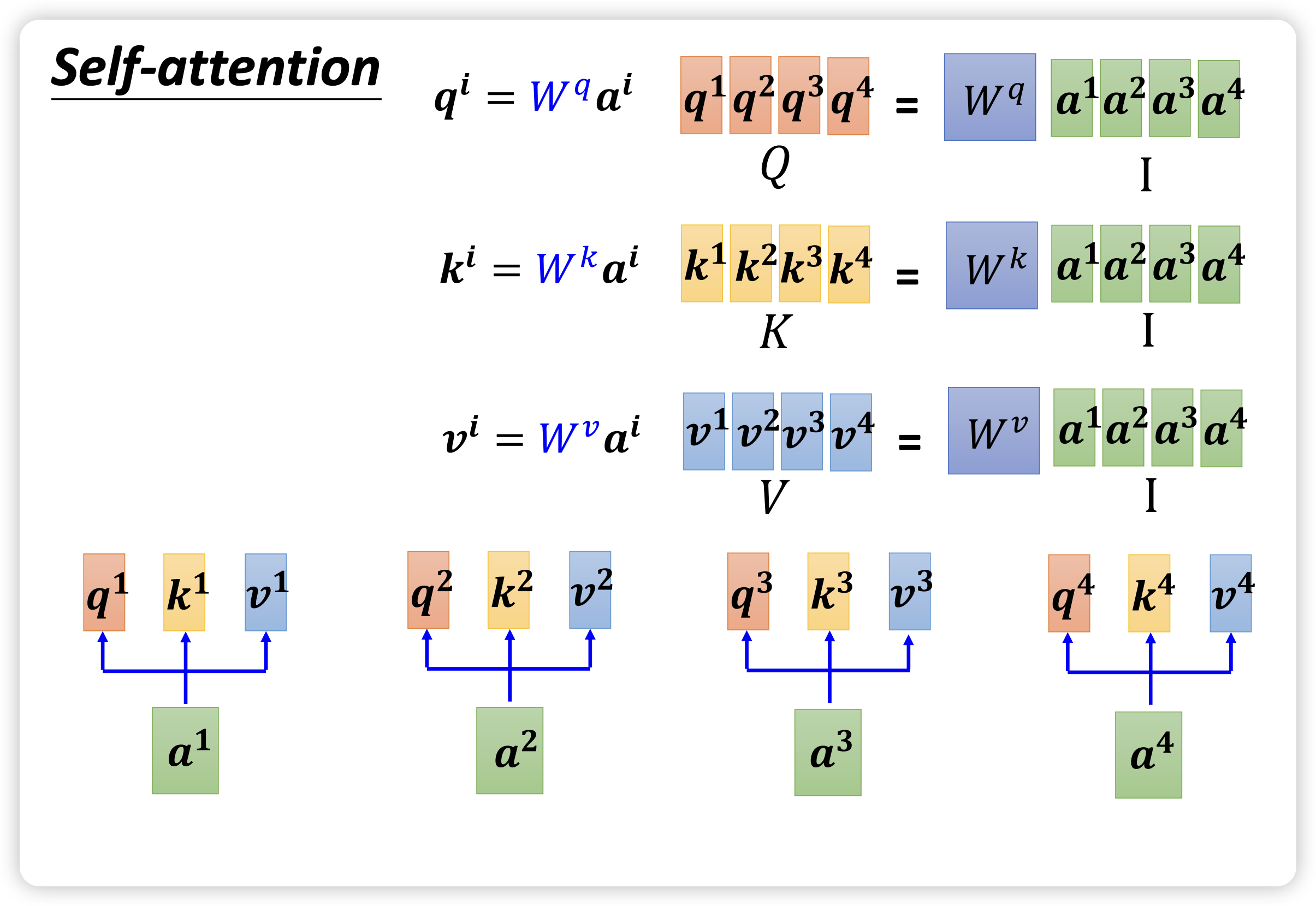
对应成矩阵形式，我们需要 3 个矩阵 $W^q$，$W^k$，$W^v$，每个矩阵的维度都是 (hidden size, hidden size)，而输出 sequence 的维度是 (sequence length, hidden size)。再考虑到 batch size 的维度，实际维度为 (batch size, sequence length, hidden size)

一般情况下，为了加速训练和识别不同类型的相关性，会使用 multi-head self-attention，如下图所示。每个 head 都有自己的 $W^q$，$W^k$，$W^v$ 矩阵，用于生成自己的 $Q$、$K$、$V$ 向量，并计算出每个 head 自己的结果。最终将各个 head 的结果 concat 连接起来，通过一个 $W^o$ 矩阵转换成最终总输出。

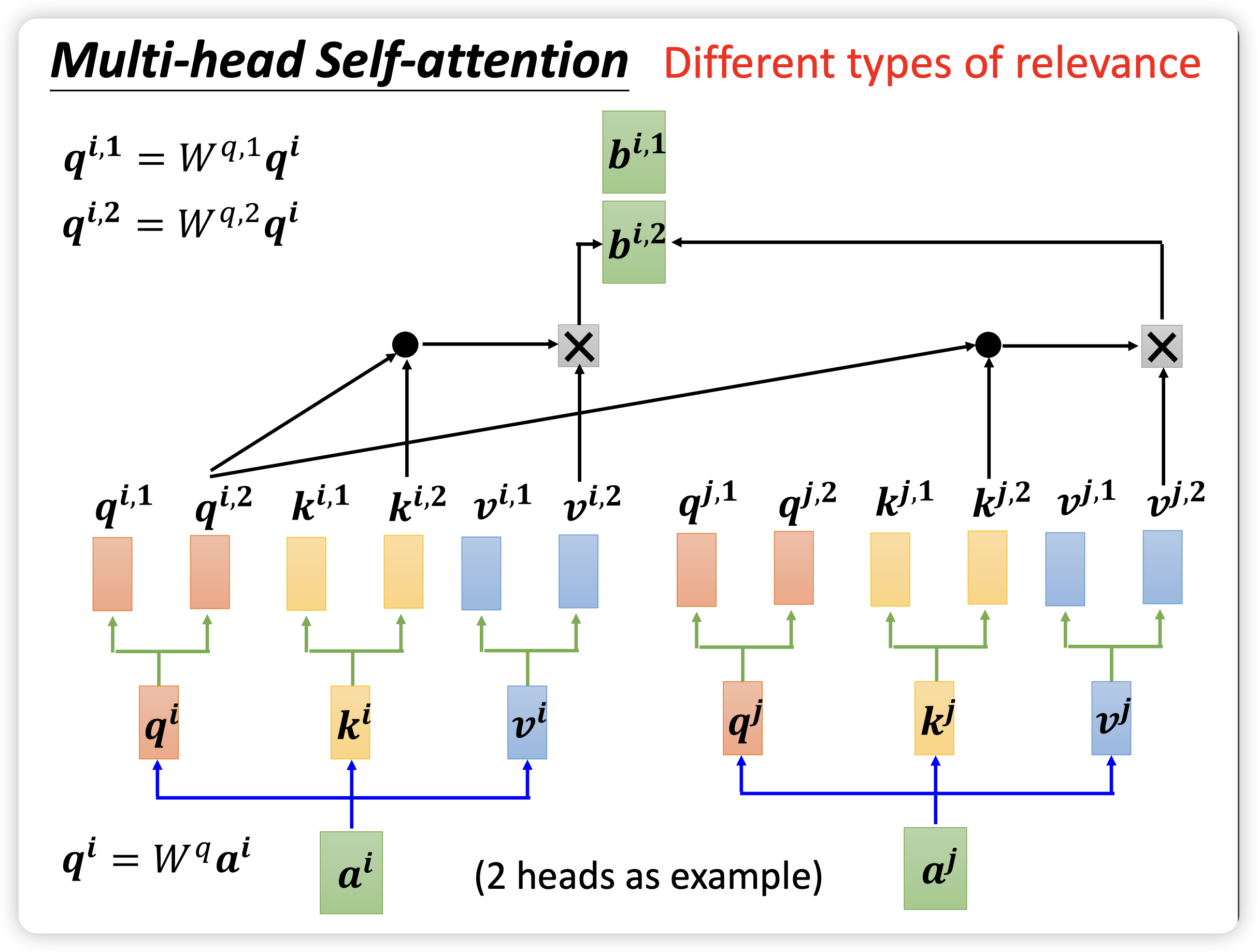
这样，multi-head self-attention 的每个 $W^q$，$W^k$，$W^v$ 矩阵的维度为 (hidden size, hidden size//num_heads)。按照这个规则拆分，multi-head 的运算量和原来单头运算量一样。

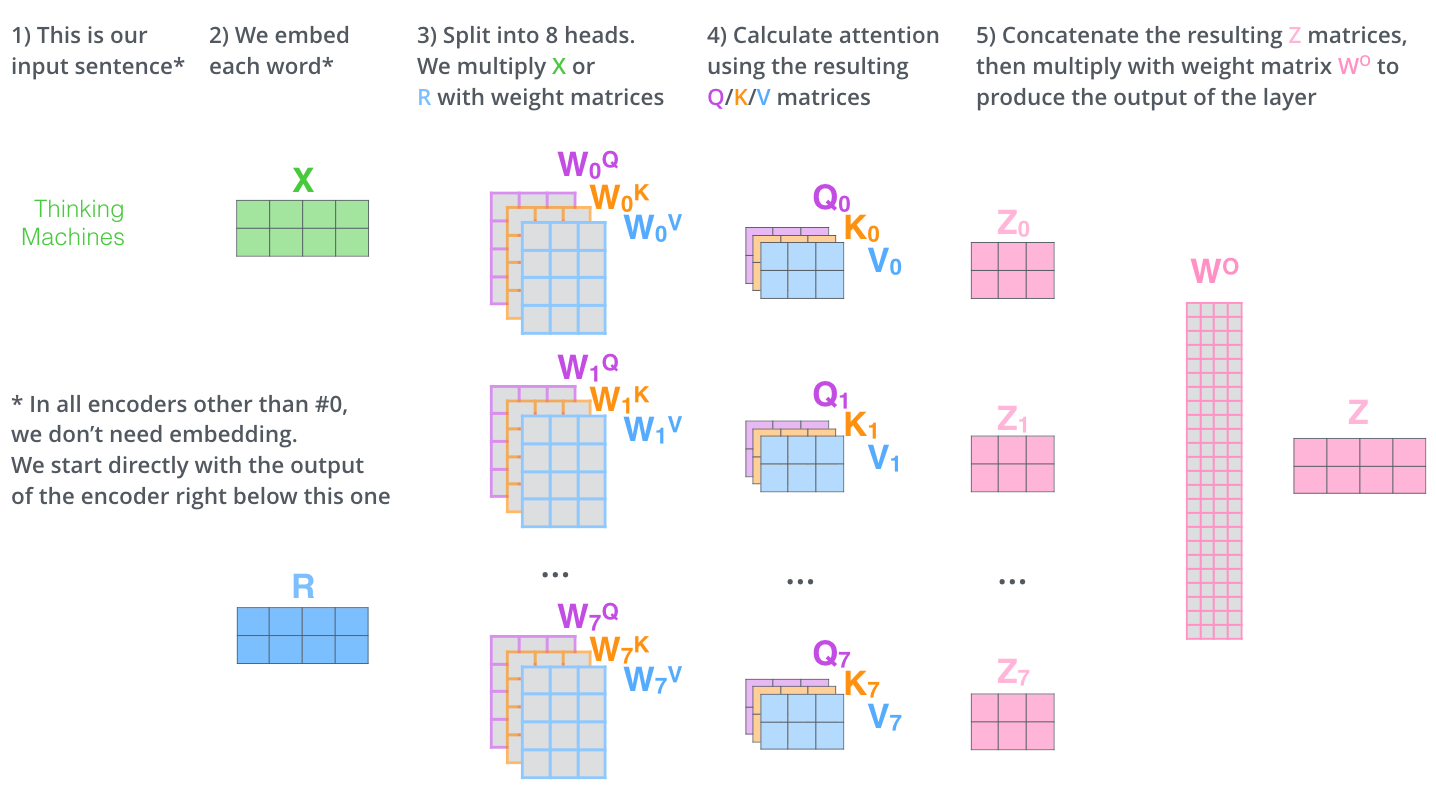
此外，为了屏蔽掉将来 token 对当前 token 的影响，计算出 attention score 后还会加上一个 mask 矩阵，把一半抹成 0。

经过上面的解释之后，下面的代码就清晰的多了。可以看到，Attention 中每个 head 需要有 $W^q$，$W^k$，$W^v$ 三个矩阵，矩阵形状为 $(C, h_s)$ ，偏置维度为 $h_s$。所有 head 参数量为 $n_{head} * 3 * (C * h_s + h_s) = 3C^2+3C$。还有一个输出矩阵 $W^o$，权重矩阵形状为 $(C, C)$ ，偏置维度为 $(C)$。因此 Attention 总的参数量为 $4C^2+4C$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class CausalSelfAttention(nn.Module):
    def __init__(self, config):
        super().__init__()
        assert config.n_embd % config.n_head == 0
        # key, query, value projections for all heads, but in a batch
        self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd, bias=config.bias)
        # output projection
        self.c_proj = nn.Linear(config.n_embd, config.n_embd, bias=config.bias)
        # regularization
        self.attn_dropout = nn.Dropout(config.dropout)
        self.resid_dropout = nn.Dropout(config.dropout)
        self.n_head = config.n_head
        self.n_embd = config.n_embd

    def forward(self, x):
        B, T, C = x.size() # batch size, sequence length, embedding dimensionality (n_embd)

        # calculate query, key, values for all heads in batch and move head forward to be the batch dim
        q, k, v  = self.c_attn(x).split(self.n_embd, dim=2)
        k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)

        # causal self-attention; Self-attend: (B, nh, T, hs) x (B, nh, hs, T) -> (B, nh, T, T)
        # manual implementation of attention
        att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
        att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
        att = F.softmax(att, dim=-1)
        att = self.attn_dropout(att)
        y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)

        y = y.transpose(1, 2).contiguous().view(B, T, C) # re-assemble all head outputs side by side

        # output projection
        y = self.resid_dropout(self.c_proj(y))
        return y

基于这段代码，我们可以非常明确地算出 Attention 中的计算量。

对于 $A \in {\Reals} ^{m\times n}$ ，$B \in {\Reals} ^{n\times l}$ ，计算 $AB$ 的一个元素需要 n 次乘法和 n-1 次加法，即 $2n-1$ FLOPs 。完成整个矩阵运算需要 $ml*(2n-1)$ ，近似为 $2mnl$ FLOPs

对 Attention，输入数据 $x$ 维度是 $(B, T, C)$，需要进行以下计算：

$$Q = xW^q, K = xW^k, V = xW^v$$

$$Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{h}}) V$$

$$x_{out} = Attention* W^o + x$$

1. 计算 $Q$，$K$，$V$，输入维度为 $(B,T,C) * (C, C)$，输出维度为 $(B, T, C)$，计算量为 $3*2BTC^2 = 6BTC^2$ FLOPs
2. 计算 $QK^T$，输入维度为 $(B, n_{head}, T, h_s) * (B, n_{head}, h_s, T)$ ，输出维度为 $(B, n_{head}, T, T)$，计算量为 $2Bn_{head}T^2*h_s=2BT^2C$
3. 计算 Softmax
4. 计算 Attention Score 和 $V$ 加权求和，输入维度为 $(B, n_{head}, T, T) * (B, n_{head}, T, h_s)$，输出维度为 $(B, n_{head}, T, h_s)$，计算量为 $2Bn_{head}T^2*h_s=2BT^2C$
5. Attention 后的线性映射，输入维度为 $(B, T, C) * (C, C)$，输出维度为 $(B, T, C)$，计算量为 $2BTC^2$

MLP Layer

最后的 MLP 层比较简单，先经过一个全连接层维度从 n_embd 升到 4*n_embd ，然后经过激活函数 Gelu，接下来经过另一个全连接层维度从 4*n_embd 降到 n_embd，最后经过一个 dropout。

可以看到，MLP 层第一个全连接层权重矩阵维度为 $(C, 4C)$ ，偏置维度为 $(4C)$ ，第二个全连接层权重矩阵维度为 $(4C, C)$，偏置维度为 $(C)$。因此 MLP 层参数量为 $8C^2+5C$ 。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class MLP(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.c_fc    = nn.Linear(config.n_embd, 4 * config.n_embd, bias=config.bias)
        self.gelu    = nn.GELU()
        self.c_proj  = nn.Linear(4 * config.n_embd, config.n_embd, bias=config.bias)
        self.dropout = nn.Dropout(config.dropout)

    def forward(self, x):
        x = self.c_fc(x)
        x = self.gelu(x)
        x = self.c_proj(x)
        x = self.dropout(x)
        return x

基于这段代码，我们可以非常明确地算出 MLP 中的计算量。

1. 第一个全连接层，输入维度为 $(B, T, C) * (C, 4C)$，输出维度为 $(B, T, 4C)$，计算量为 $8BTC^2$
2. 第二个全连接层，输入维度为 $(B, T, 4C) * (4C, C)$，输出维度为 $(B, T, C)$，计算量为 $8BTC^2$

结合 Attention ，可以快速得到 Transformer 每一层需要的计算量为 $24BTC^2+4BT^2C$

Summarize

Note

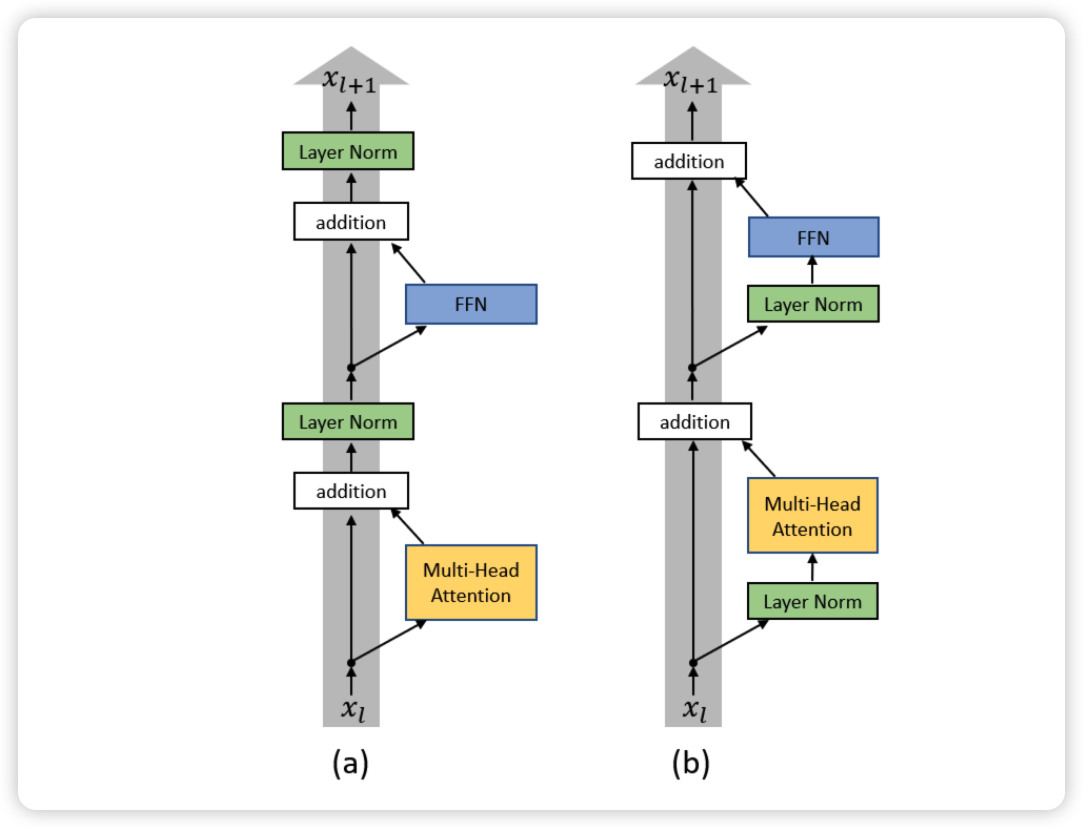
前面讲述的是以 GPT 为代表的 decode-only 的 transformer 架构，和 Attention is All You Need 论文⁷ 的 transformer 架构还不完全一样。

比如这里 LayerNorm 的位置，到底是应该先算完 Attention 和 MLP 之后再做 LayerNorm，还是先做 LayerNorm 再算 Attention 和 MLP。论文 On Layer Normalization in the Transformer Architecture¹⁷ 就对这个问题做了进一步的分析，本文中也采用的是 Pre-LayerNorm 的架构。

Parameters

对 Transformer 每一层，Attention 参数量为 $4C^2+4C$，MLP 参数量为 $8C^2+5C$ 。除此之外，Attention 和 MLP 层各有一个 LayerNorm，包括两个可训练参数：缩放系数 $\gamma$ 和平移参数 $\beta$，维度都是 $(C)$ 。两个 LayerNorm 的参数量为 $4C$。因此，Transformer 每一层参数量为 $12C^2+13C$。

除此之外， wte 参数量为 $VC$ ，wpe 参数量为 $TC$，一般 $TC$ 相对 $VC$ 可以被忽略。

因此，总的参数量为 $l(12C^2+13C)+VC$ ，忽略一次项，模型参数量近似为 $12lC^2$。

FLOPs

对 Transformer 每一层，计算量为 $24BTC^2+4BT^2C$。

在输出 logits 的计算中，需要将隐藏向量映射为词表大小。矩阵输入维度为 $(B, T, C)*(C, V)$，输出为 $(B, T, V)$，计算量为 $2BTCV$

因此，总的计算量为 $l(24BTC^2+4BT^2C)+2BTCV$ 。当隐藏层维度 $C$ 比较大，且远大于 Sequence Length $T$ 时，可以忽略一次项，计算量近似为 $24lBTC^2$。

结合前面模型参数量为 $12lC^2$，输入的 tokens 数为 $BT$，存在 $\frac{24lBTC^2}{12lC^2 * BT} = 2$。这部分即是重新展示了 疯狂的 H100：现代 GPU 体系结构浅析，从算力焦虑开始聊起 中提到的计算过程：

Scaling Law 论文 Section 2.1 对于这个公式的做了简单的推导，在 forward pass 需要的 FLOPs 数为 $C_{forward} = 2 * P * N$

如下图所示：

Memory Access

在上一小节根据 nanoGPT 再次回顾了下 decoder-only 的 transformer 模型结构之后，关于 GPT 系列模型对应的计算量、内存占用也能够很快地计算出来了。如前所述，在模型计算中，不仅仅要考虑到内存容量，还需要考虑内存访问。

在 疯狂的 H100：现代 GPU 体系结构浅析，从算力焦虑开始聊起 我们看到，类似于 CPU 内存体系，GPU 也存在明显的 Memory Hierarchy，GPU 能够访问的内存是由不同层级不同大小和不同读写速度的内存组成。

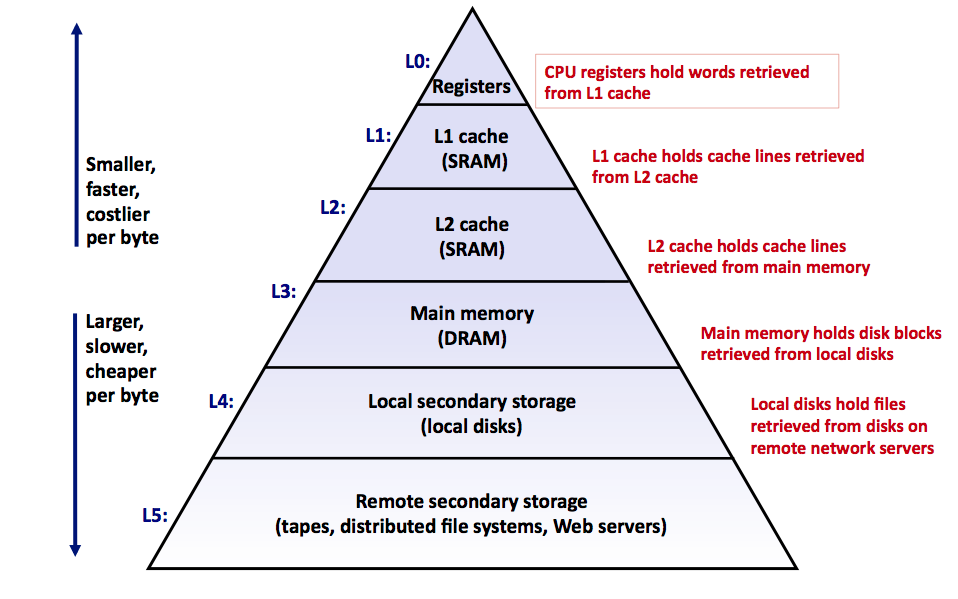
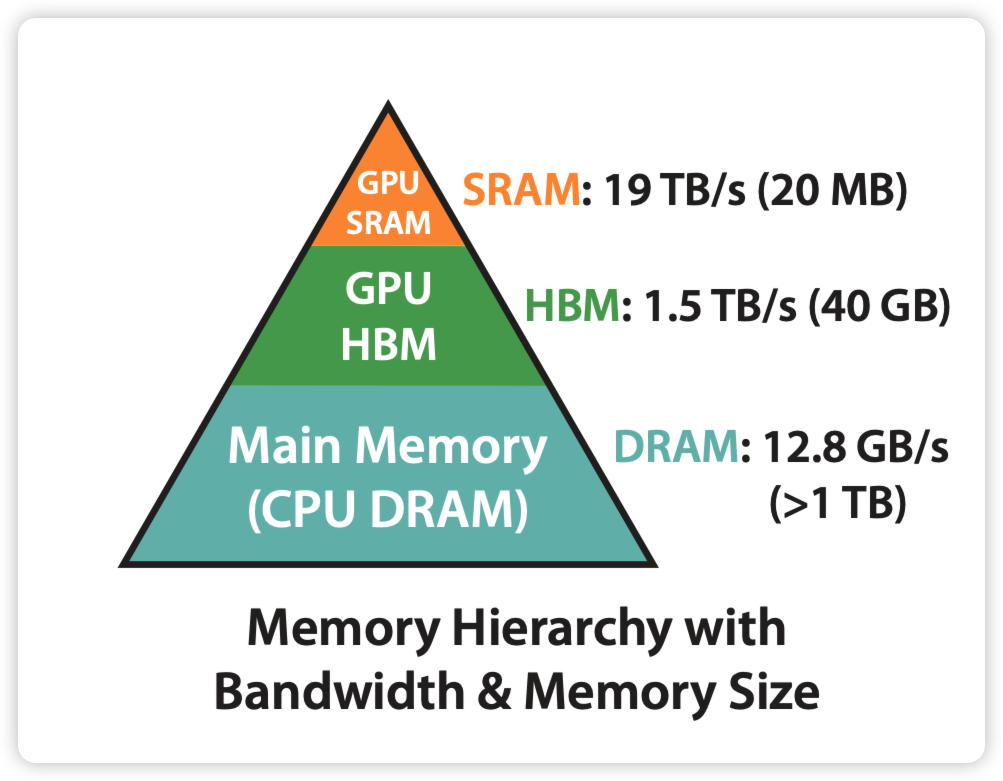
从编程模型看，GPU 的内存模型可以分为两级，以 H100 为例：

• Global Memory： 包括 80GB 的 HBM3 存储和 50MB 的 L2 Cache
• Shared Memory：每个 SM 中共享的 256KB L1 Cache/Shared Memory，每个 Thread 中共享的 1KB RegisterFile

  

以 H100 PCIe 为例，以下表格显示了不同层级的内存访问速度，数据来源¹⁸：

不同层级的 Memory 访问速度的不同，会显著影响到应用程序的性能。根据程序计算模式的不同，一般可以分为两种：

• Compute Bound：性能受限于硬件本身算力上限 $\pi$ ，单位是 FLOPS
• Memory Bound：性能受限于硬件本身带宽上限 $\beta$ ，单位是 byte/s

如何区分程序是 Compute Bound 还是 Memory Bound 呢？可以通过计算该程序所需的总运算量 $\pi_t$ 和所需的总数据读取量 $\beta_t$ 来对比硬件本身性能。

• 当计算所需时间 $\frac{\pi_t}{\pi}$ 大于访存所需时间 $\frac{\beta_t}{\beta}$，说明受限于算力，为 compute bound
• 当计算所需时间 $\frac{\pi_t}{\pi}$ 小于访存所需时间 $\frac{\beta_t}{\beta}$，说明受限于访存，为 memory bound

这即是 Roofline Model¹⁹ 所指明的结论，在某个硬件上，任何程序所能够达到的最高算力为 P。当该程序的计算强度大于硬件最大计算强度 $I_{max} = \frac{\pi}{\beta}$，单位为 FLOP/Byte，程序所能达到算力 Roofline 为 $\pi$ ，这种场景为 compute bound。否则，该程序受限于访存，为 memory bound。

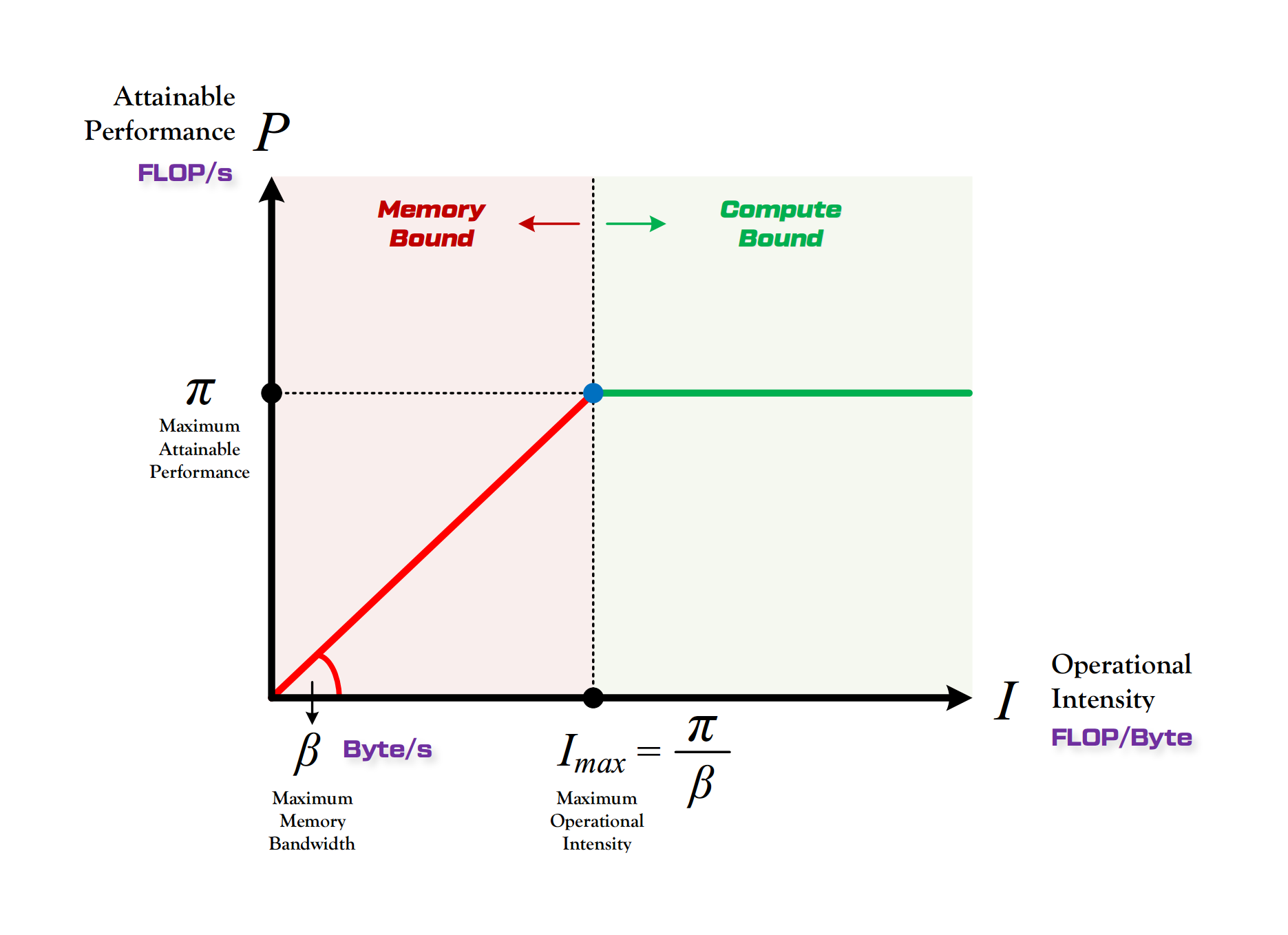
• Attention 中和后续的全连接层大量的矩阵计算 GEMM 为 compute bound
• 而像激活函数、dropout、mask、softmax 和 LayerNorm 等一般是 memory bound

如果能够综合考虑在 Attention 计算中硬件访存对于计算性能的限制，将极大提升模型训练的性能，对于解决目前大模型应用中上下文长度受限的问题也能够有很大的帮助。FlashAttention 系列⁸²⁰即是这一方向非常优秀的工作。

FlashAttention

FlashAttention 论文开篇即指出，当 sequence length 增加时，模型计算量和存储占用复杂度随着序列长度呈二次方增长，具体计算在前面已经推导过了，此处不再详述，可以参考这篇文章²¹。本节采用的数学符号表示如下：

这里的内存占用 $N^2$ 的关键，就在于 Attention Score $S = Q^KT$ 的计算，当 sequence length 增加时，显存占用以 $O(N^2)$ 比例增加。FlashAttention 优化的思路，就是通过 Tiling 切块，将大矩阵切成小矩阵运算，减少中间内存占用。Tiling 是矩阵计算中常见的优化思路，Attention 的主要问题是 Softmax 的计算限制了必需要等待整行的计算结果才能够继续计算，这大大限制了 Attention 的分块并行计算。

为了解决这个问题，FlashAttention 在 Online Softmax²² 和 Memory-Efficient Attention²³ 的基础上，进一步优化了 Memory READ/WRITE 的次数，通过 Tiling 省去了中间 S 矩阵的内存占用，保证了最终结果 O 矩阵的正确性，并在反向中通过冲计算来节省内存。

具体的公式推导可以参照 From Online Softmax to FlashAttention²⁴ 这篇文章，十分简洁清晰，强烈推荐。看完后再对着原始论文和这几篇文章²⁵²⁶ 整个过程包括前向和反向 tiling 就比较清楚了，核心原理如下图所示。通过 FlashAttention，我们可以不用关注中间计算过程中 O 矩阵的正确性，只需要保证最终的 O 矩阵正确即可。

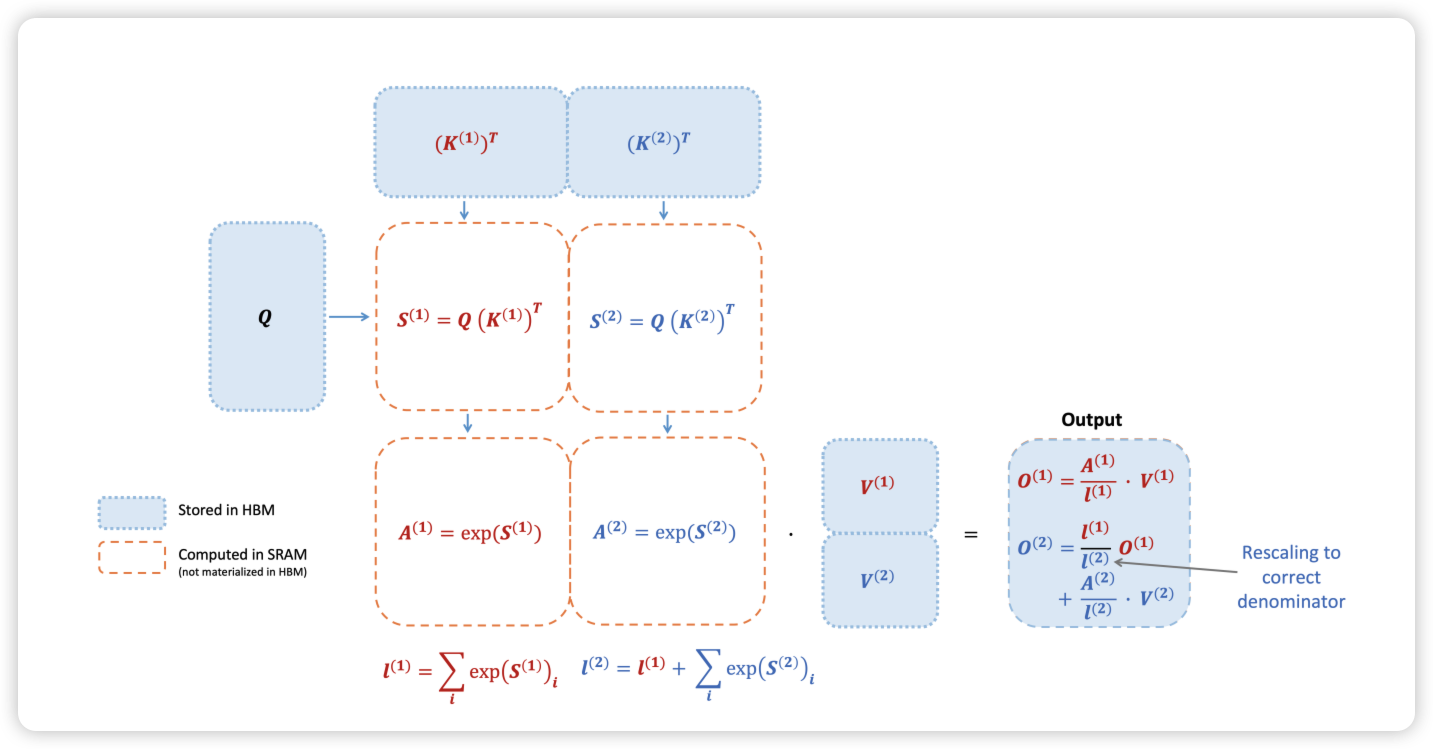
FlashAttention-2 相对于 FlashAttention-1，进一步改变了 Tiling 的顺序，将 Q 矩阵的循环挪到了最外层，这样就可以将 Q 矩阵的循环交给 Thread Block 来并行计算。也就是说，除了原来 batch 和 head 两个维度可以并行，现在也可以在 sequence 维度切分，三层循环分给不同的 thread block，进一步增加 GPU 的吞吐。

循环顺序调换之后，进一步的对同一个 block 中的 warp patition 做了优化，将 V1 版本中沿着 K 切共享 Q 变成 V2 中沿着 Q 切共享 K。每个 warp 执行矩阵乘法以获得 $QK^T$ 的切片，然后只需与 V 的共享切片相乘就能获得相应的输出切片。warp 之间不需要通信，共享内存读写的减少也可以提升速度。

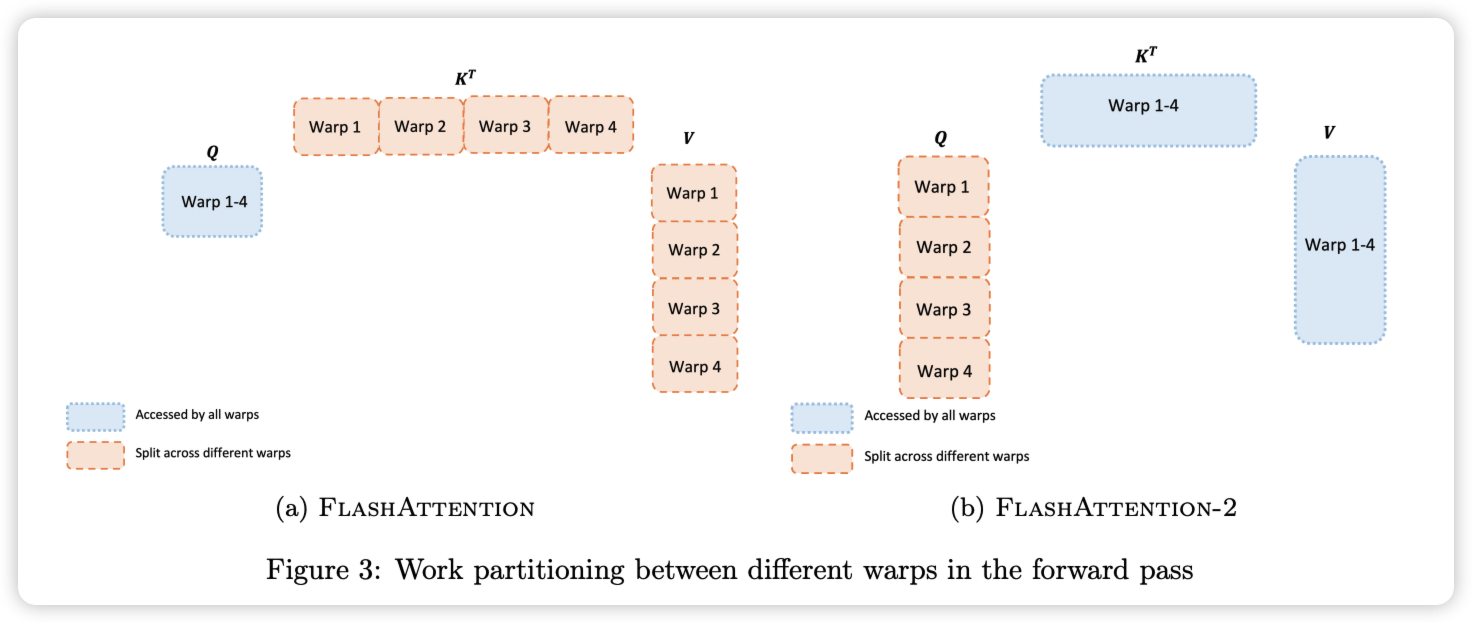
KV Cache

前面介绍了 Attention 的基础结构和类似于 FlashAttention 这样的优化算法，后面我们将主要关注于推理环节，看看推理过程中对于内存的占比。

以 GPT 为代表的 Decoder-Only 结构的 Transformer 模型推理一般分为两个步骤：

• Prefill：根据输入的 prompt 计算 KV Cache
• Decode：每次 token by token 地自回归输出 token，一次推理仅输出一个 token

如下图所示，在 Prefill 阶段中，Query 的长度与 Prompt 长度有关，计算出这里的 K 矩阵和 V 矩阵。在 Decode 阶段，每次输入只需要输入一个 token，这个 token 也就是上次推理出的 token，然后即可计算出本次推理的 token，并且同时更新 K 矩阵和 V 矩阵。

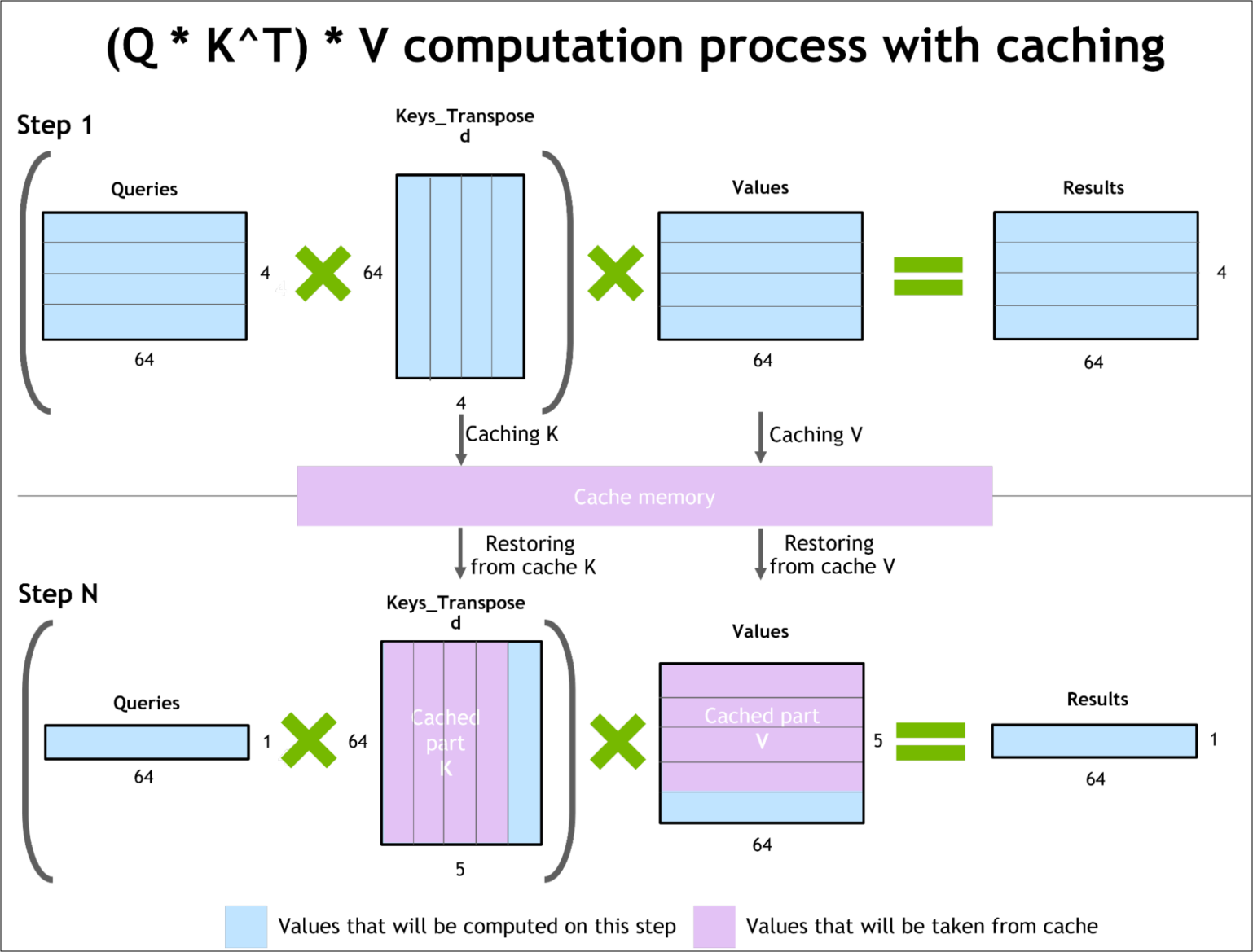
为什么使用了 KV Cache 之后，每次输入只需要前一个 token 即可推理出下一个 token？因为根据计算公式，每次 token 的 query，需要根据之前计算出来的 K 矩阵和 V 矩阵，经过 Softmax 和 V 之后才能输出结果。因为 Casual Mask 的存在，这里缓存的 K 矩阵和 V 矩阵只依赖于之前输入的 token 产生，并且可以在下一次输出复用。

$$O = softmax(\frac{QK^T}{\sqrt{d_k}}) * V$$

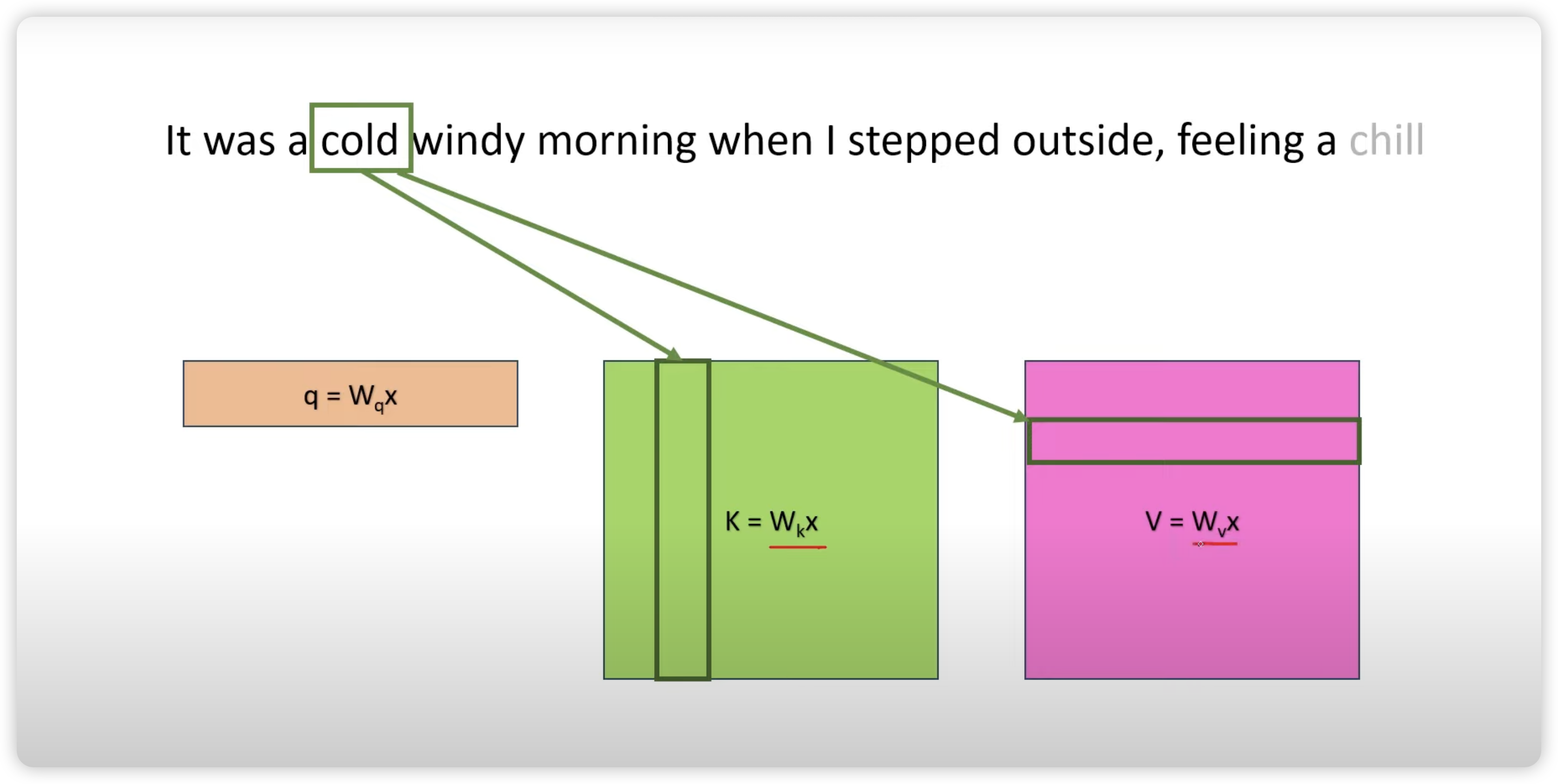
因此，根据上一个 token，可以快速算出预测出来的下一个 token，并且更新对应的 K 矩阵和 V 矩阵。具体的推导可以参见²⁷和²⁸ 两篇文档。

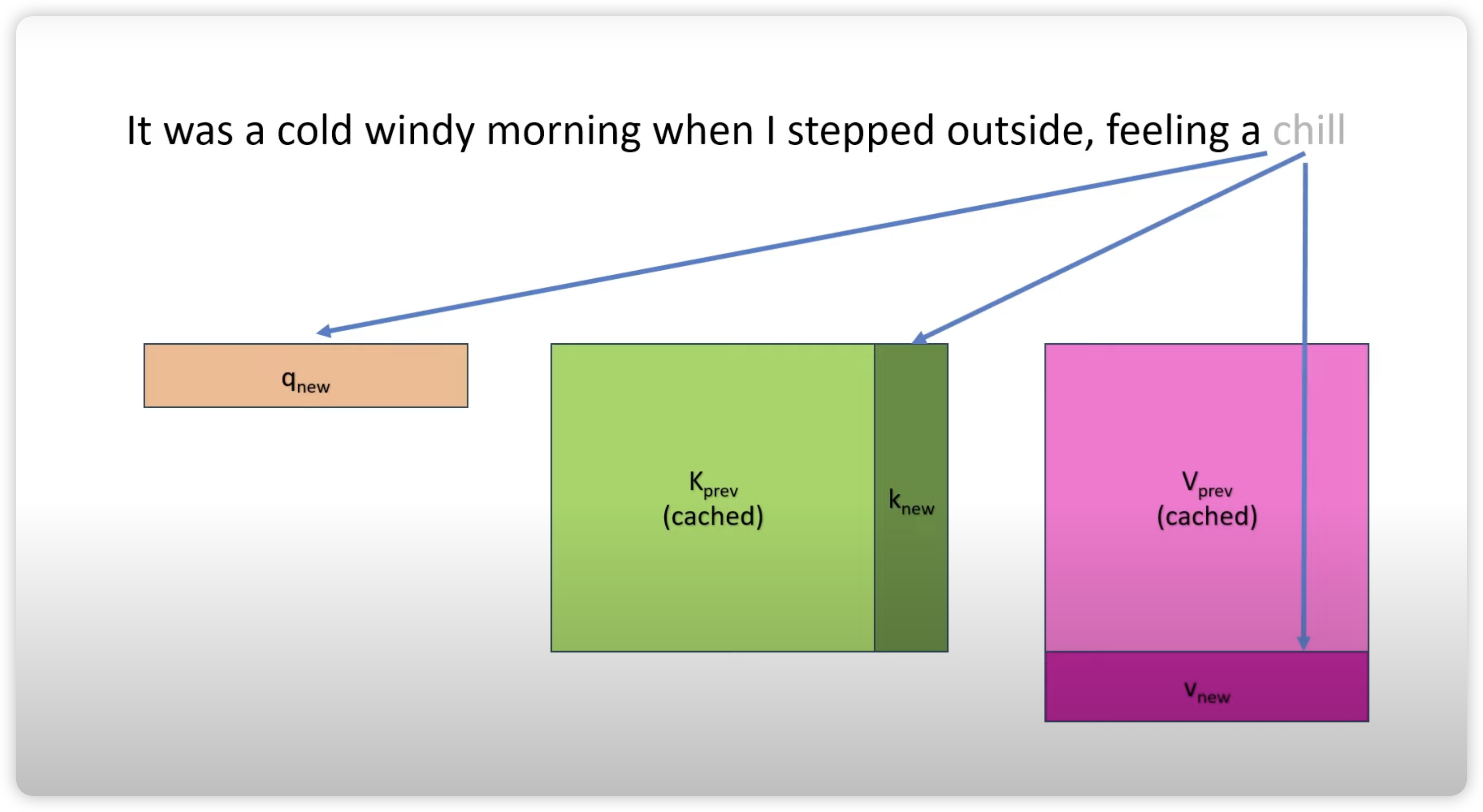
KV Cache 很好的加速了模型的推理，但是在推理过程中，模型的内存占用会与模型的上下文长度息息相关。KV Cache 具体内存占用计算方法为:

$$2 * precision* n_{layers} * d_{model} * seqlen * batch$$ 这里的 2 指的是 K 矩阵和 V 矩阵两个矩阵，一般精度为 fp16，代表两个字节。以 OPT-30B 模型为例，随着模型上下文长度和 batch size 的增大，KV Cache 的占用内存显著增大，并快速超过了模型本身。

下图则展示了在 Prefill 和 Decode 阶段，算法对于 AI Infrastructure 提出的挑战，可以看到推理 Prefill 阶段明显是 Compute Bound，而 Decode 阶段时 Memory Bound。

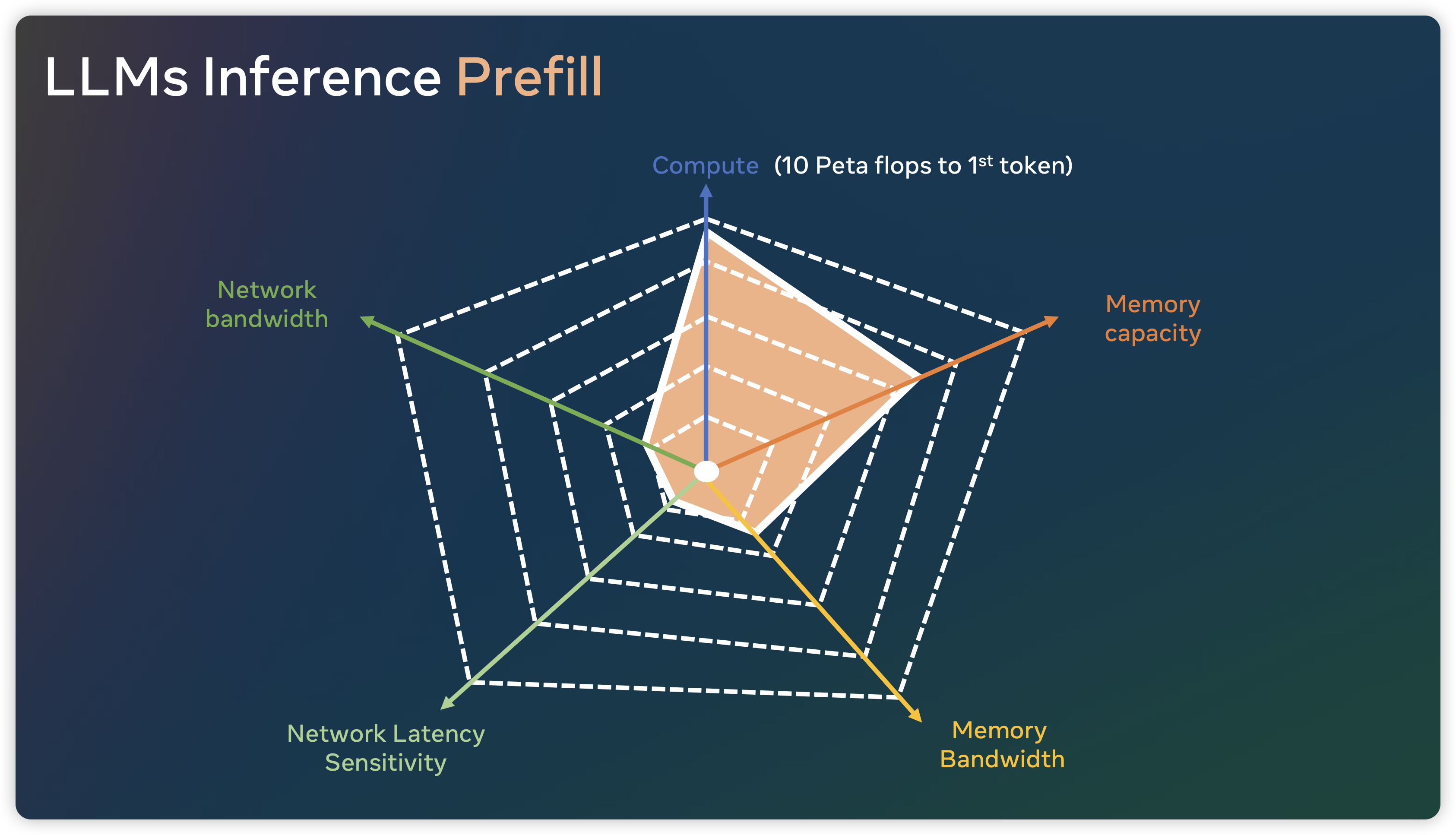
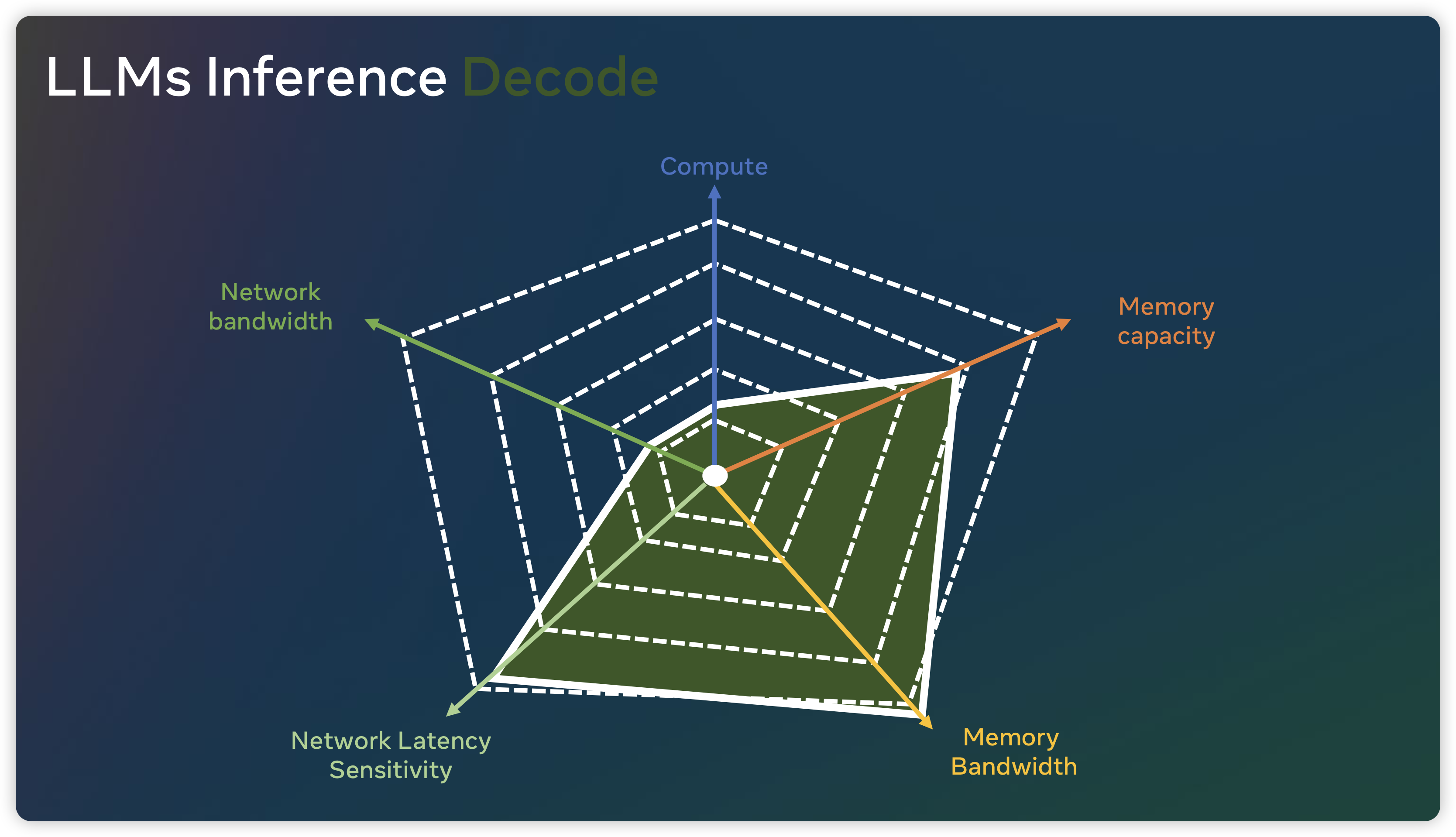
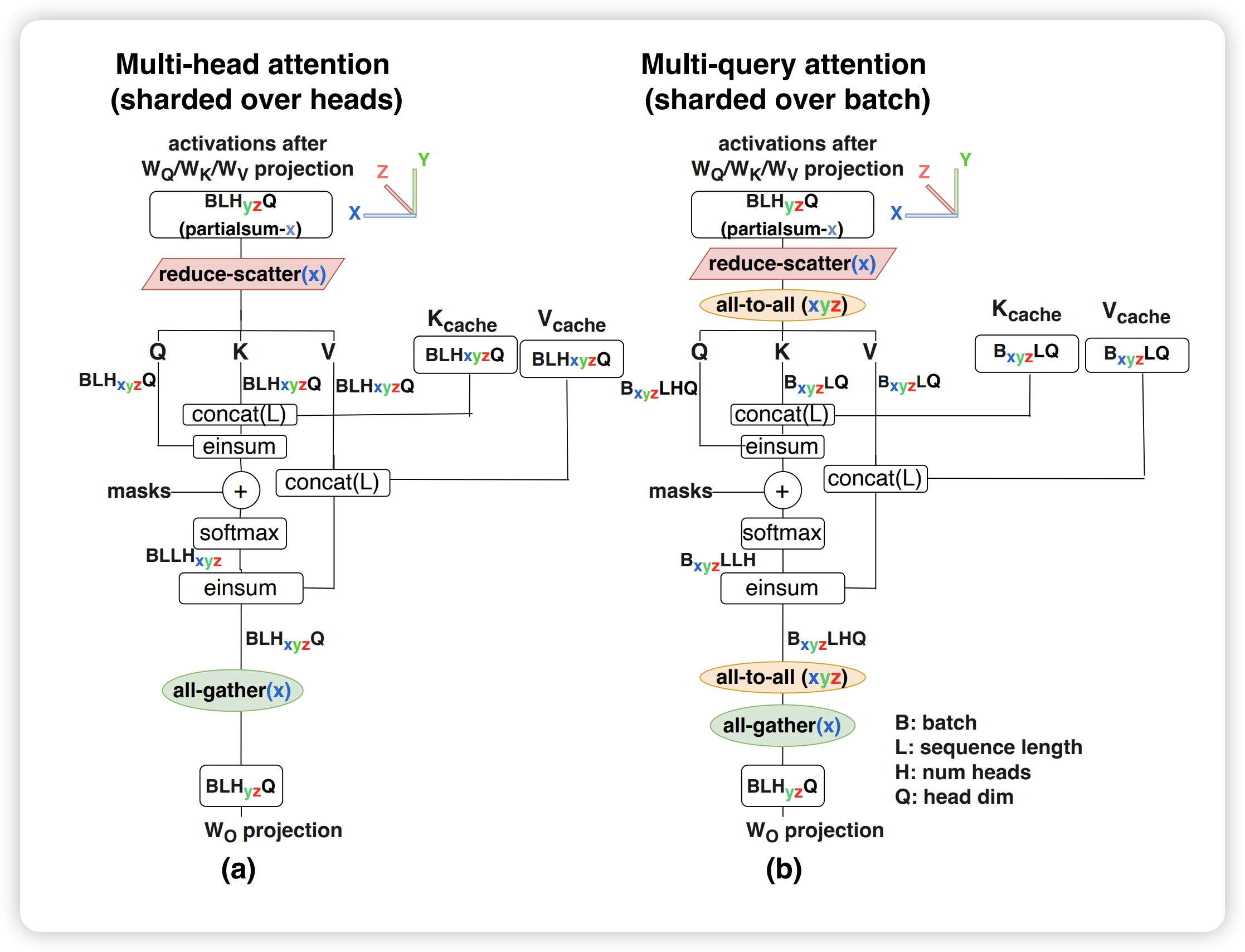
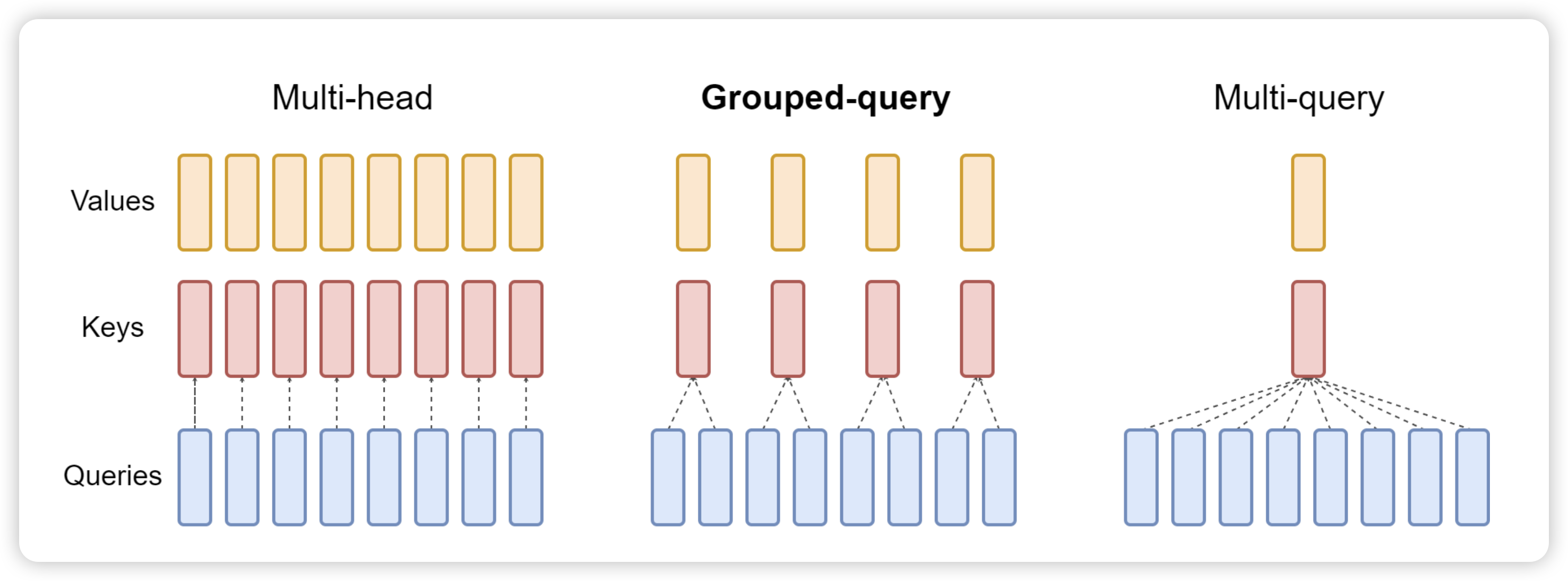
为了优化 KV Cache，一般会使用 Multi Query Attention²⁹。MQA 中不同的 head 共享一个 K 和 V，而单独保留各自 head 的 Q。与 MQA 不同， MHA 中每个 head 都有自己的 K/V/Q 矩阵。目前 SoTA 模型一般默认都会使用 MQA 来训练和推理，并且在更大模型中效果比较明显。比如 LLaMA2 7B 使用了 full attention，而 70B 使用了 MQA。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

# ref: https://zhuanlan.zhihu.com/p/659770503
# Multi Head Attention
self.Wqkv = nn.Linear(     # Multi-Head Attention 的创建方法
    self.d_model,
    3 * self.d_model,     # Q、K和V 3 个矩阵, 所以是 3 * d_model
    device=device
)
query, key, value = qkv.chunk(3, dim=2)      # 每个 tensor 都是 (1, 512, 768)

# Multi Query Attention
self.Wqkv = nn.Linear(       # Multi-Query Attention 的创建方法
    d_model,
    d_model + 2 * self.head_dim,    # 只创建Q的头向量，所以是 1* d_model, 而K和V不再具备单独的头向量, 所以是 2 * self.head_dim
    device=device,
)
query, key, value = qkv.split(
    [self.d_model, self.head_dim, self.head_dim],    # query -> (1, 512, 768), key   -> (1, 512, 96), value -> (1, 512, 96)
    dim=2
)

Grouped Query Attention³⁰ 是一种介于多头注意力和 MQA 之间的折中方案。它将 Query Heads 分组，并在每组中共享一个 Key Head 和一个 Value Head。表达能力与推理速度：GQA 既保留了多头注意力的一定表达能力，又通过减少内存访问压力来加速推理速度。

PagedAttention

除了上述的 MQA 和 GQA 之外，另一个不错的工作是 PagedAttention。以下内容来自 vLLM 官网³⁰，以后有机会进一步对源码进行解读。

PagedAttention 仿照操作系统中经典的虚拟内存和分页思想，允许在非连续的内存空间中存储连续的 Key 和 Value。具体来说，PagedAttention 将每个序列的 KV cache 划分为块，每个块包含固定数量 token 的键和值。在注意力计算期间，PagedAttention 内核可以有效地识别和获取这些块。

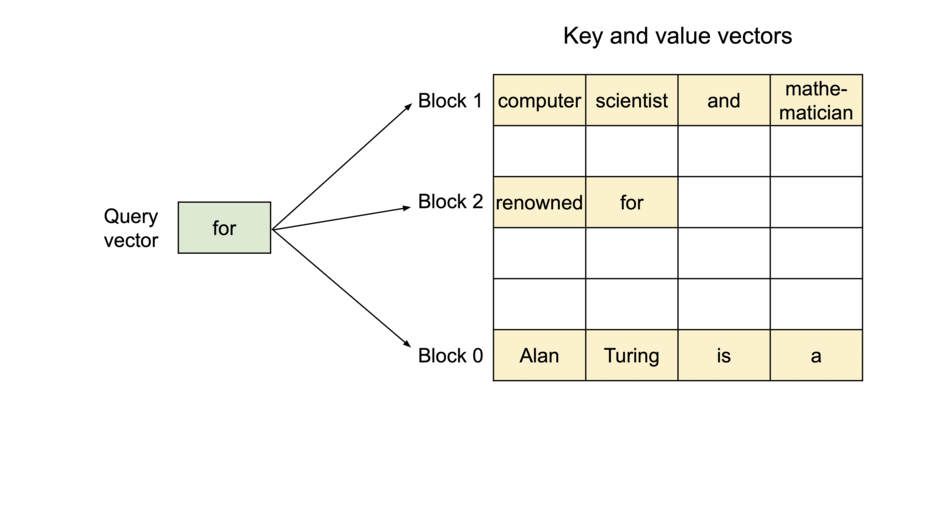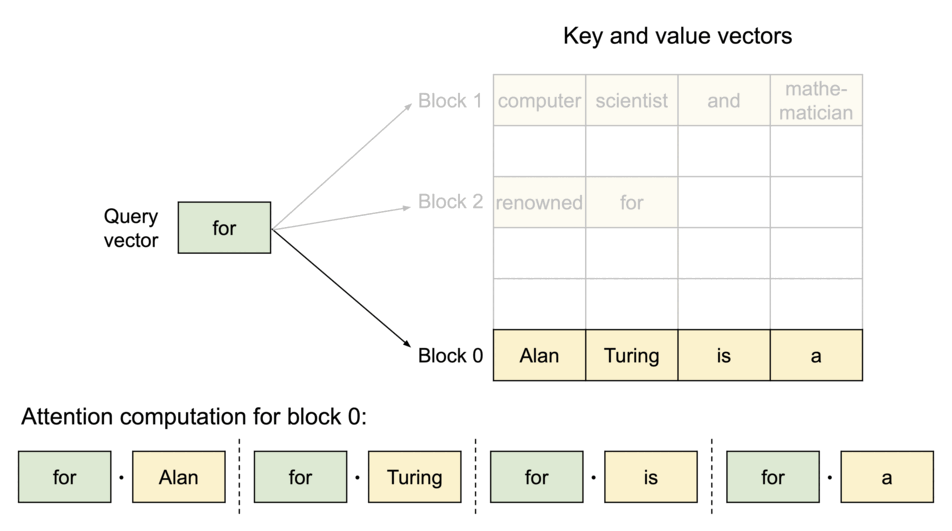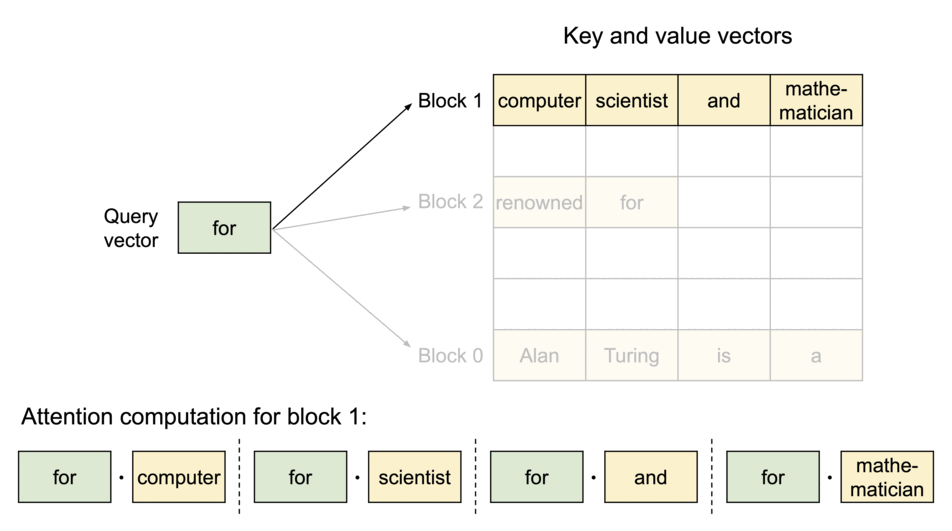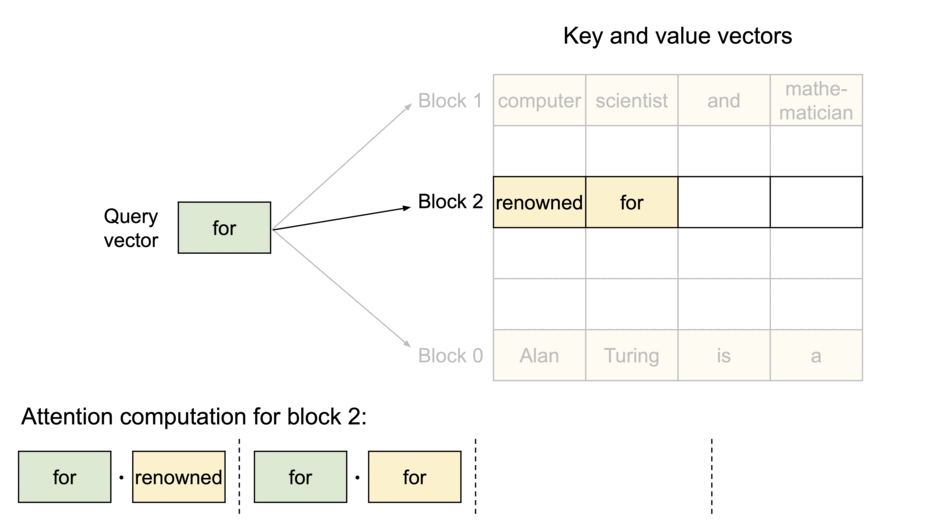
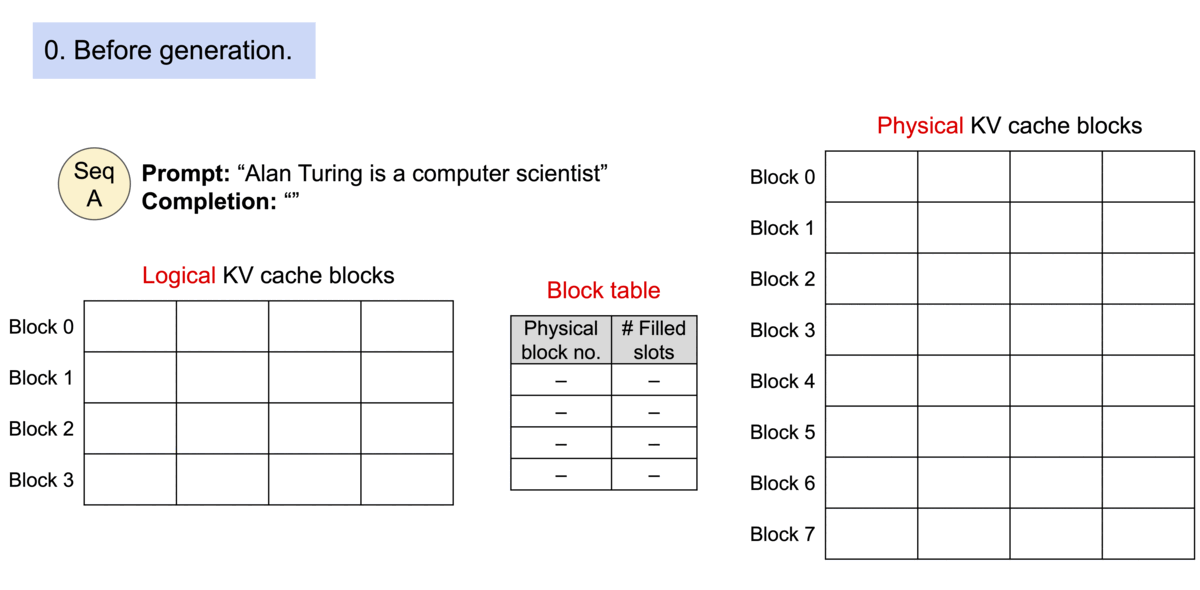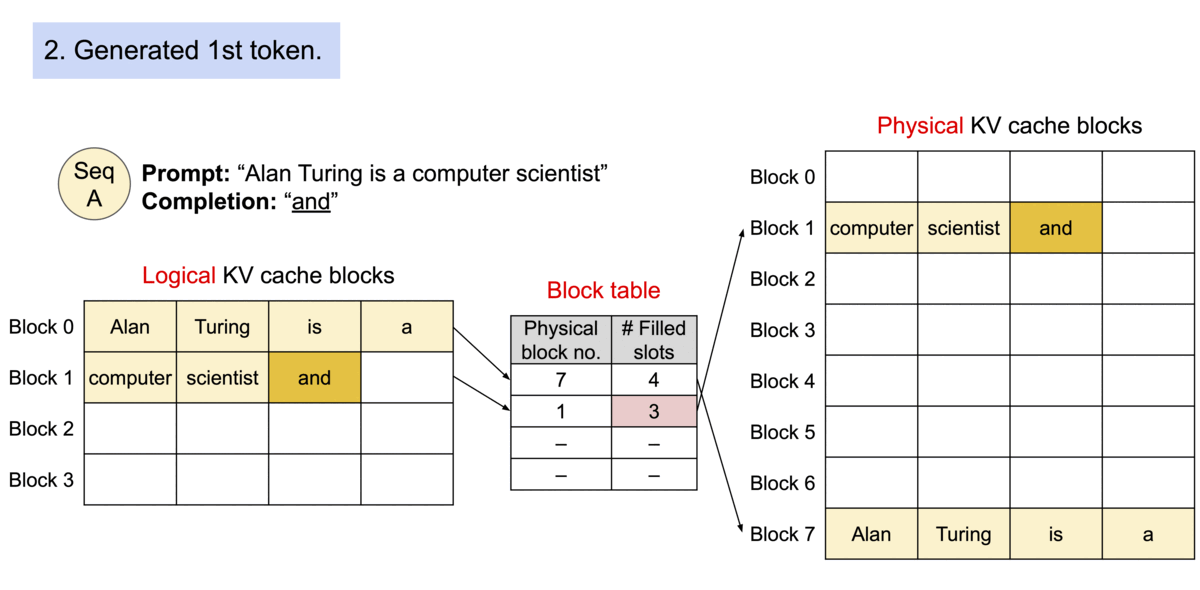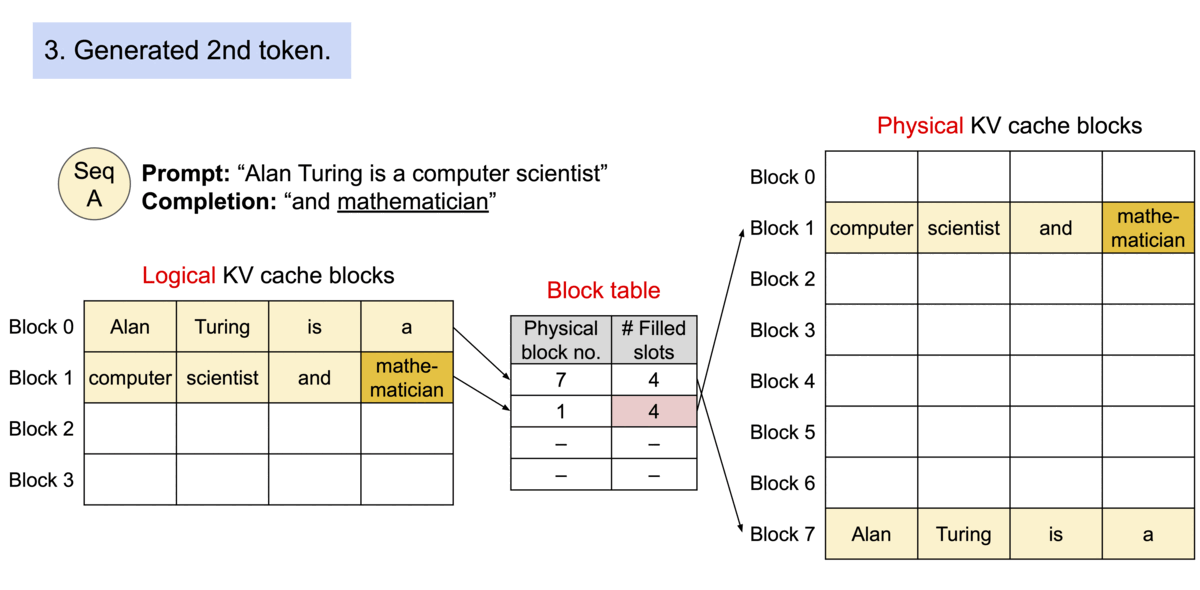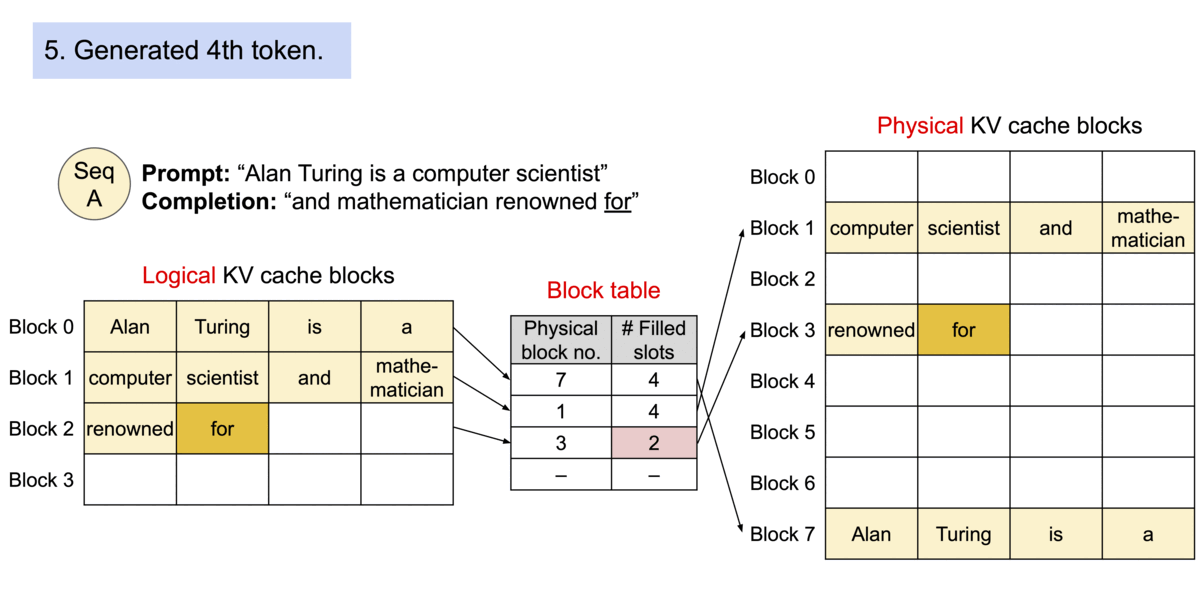
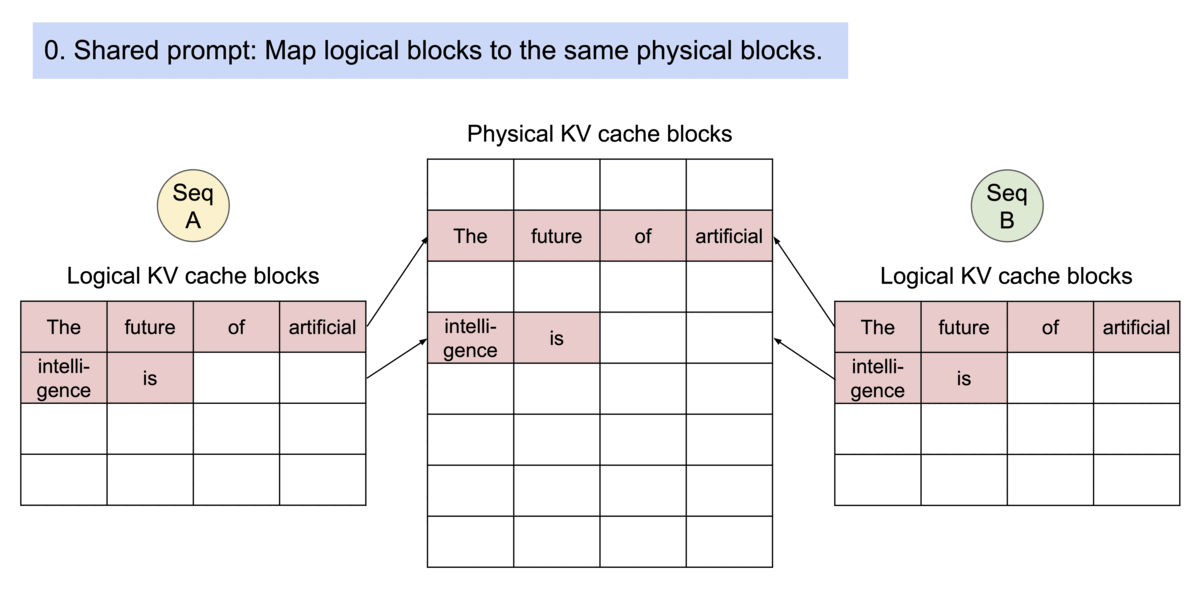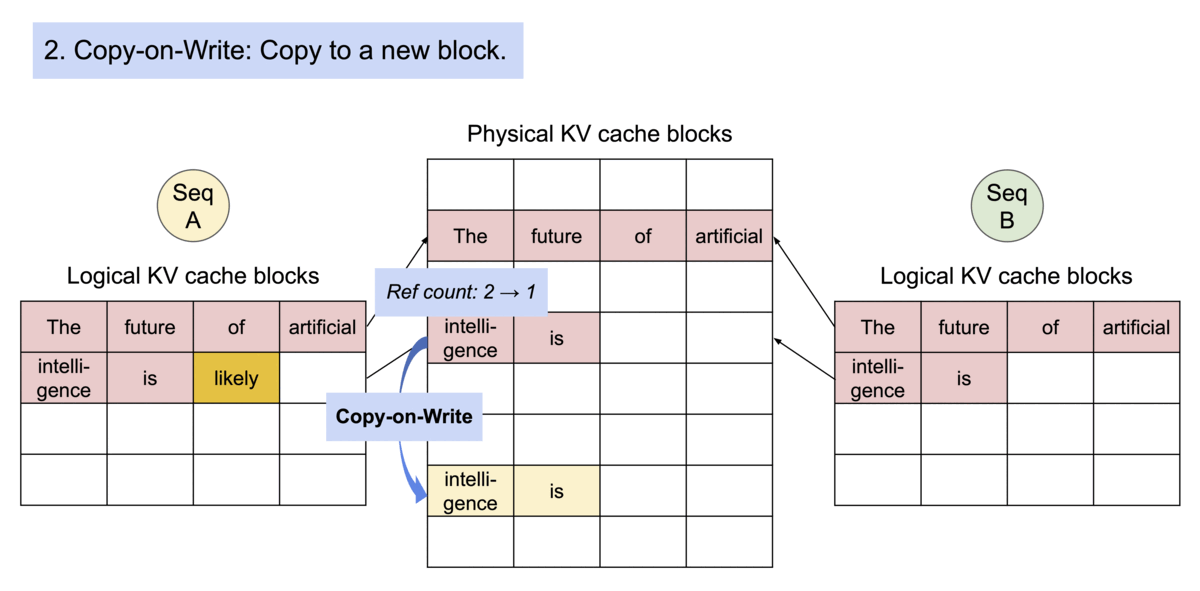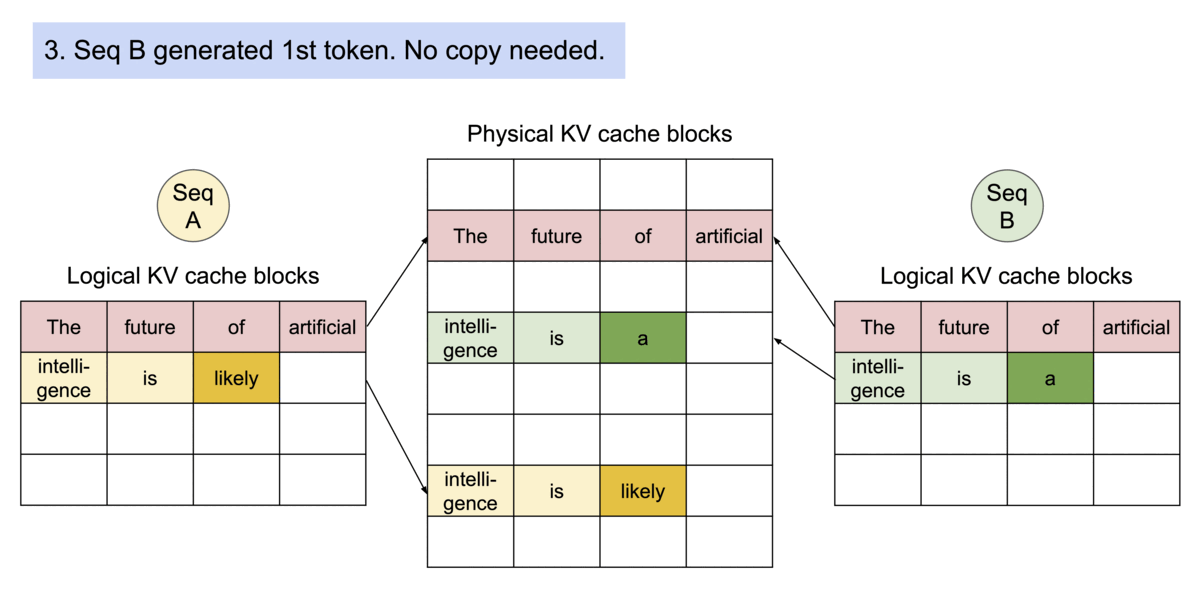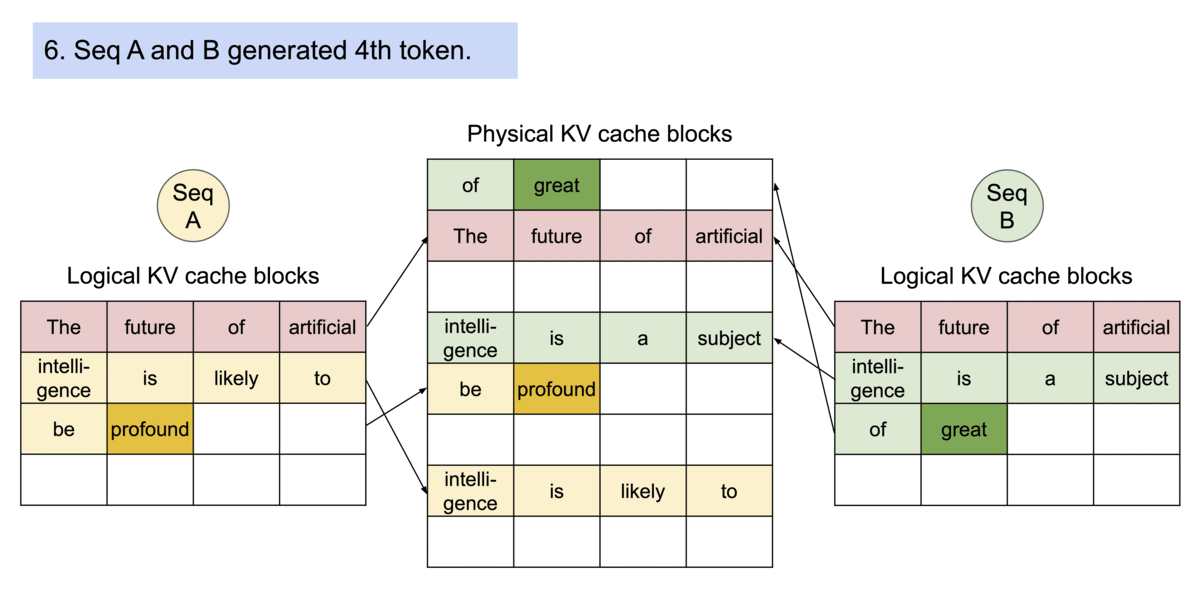
PagedAttention 自然地通过其块表格来启动内存共享。与进程共享物理页面的方式类似，PagedAttention 中的不同序列可以通过将它们的逻辑块映射到同一个物理块的方式来共享块。为了确保安全共享，PagedAttention 会对物理块的引用计数进行跟踪，并实现 Copy-on-Write 机制。

Flash Decoding

在推理阶段，Flash Attention 的作者又推出了 Flash Decoding³¹。因为在推理时候 query 的 length 通常是 1，没有 FlashAttention 2 里面的 sequence parallelism 可以使用，整个计算过程中只使用了 GPU 的一小部分。为了提升 GPU 利用率，Flash Decoding 增加了 key/value 的并行维度，将 query 复制给不同的 kv cache chunks，并行 scan 来给 online softmax 做 reduction。

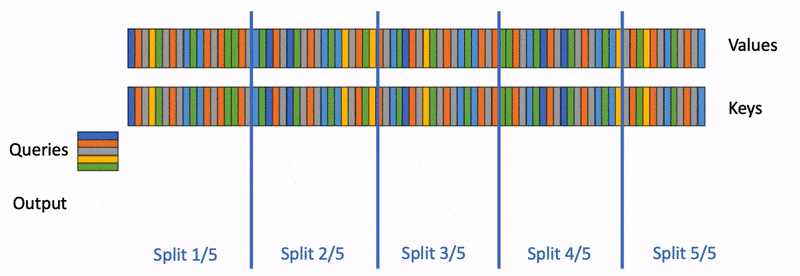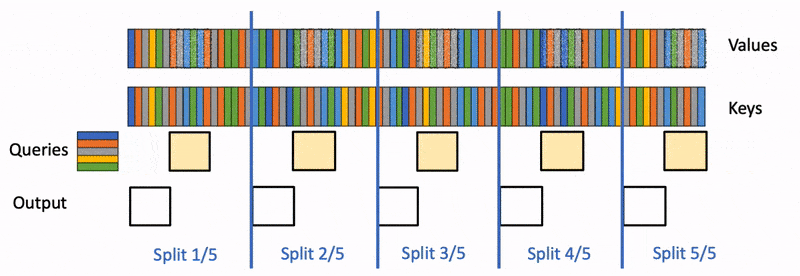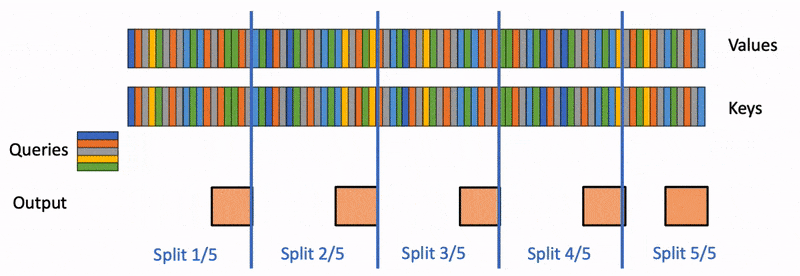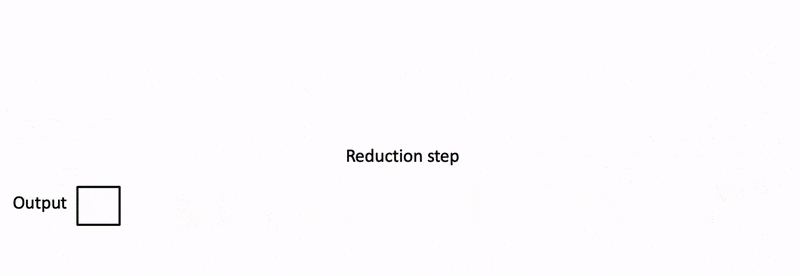
Looking Forward

本文围绕着 Attention 机制分析了当前 Transformer 模型因为 $O(N^2)$ 的复杂度带了的在训练和推理上的诸多限制。受限于目前 GPU 内存的限制，FlashAttention 和 PagedAttention 等分别给出了自己的解决方案。但是，各种优化还是阻挡不了人们对于线性复杂度的架构的追求，比如最近发表的 Mamba³²。

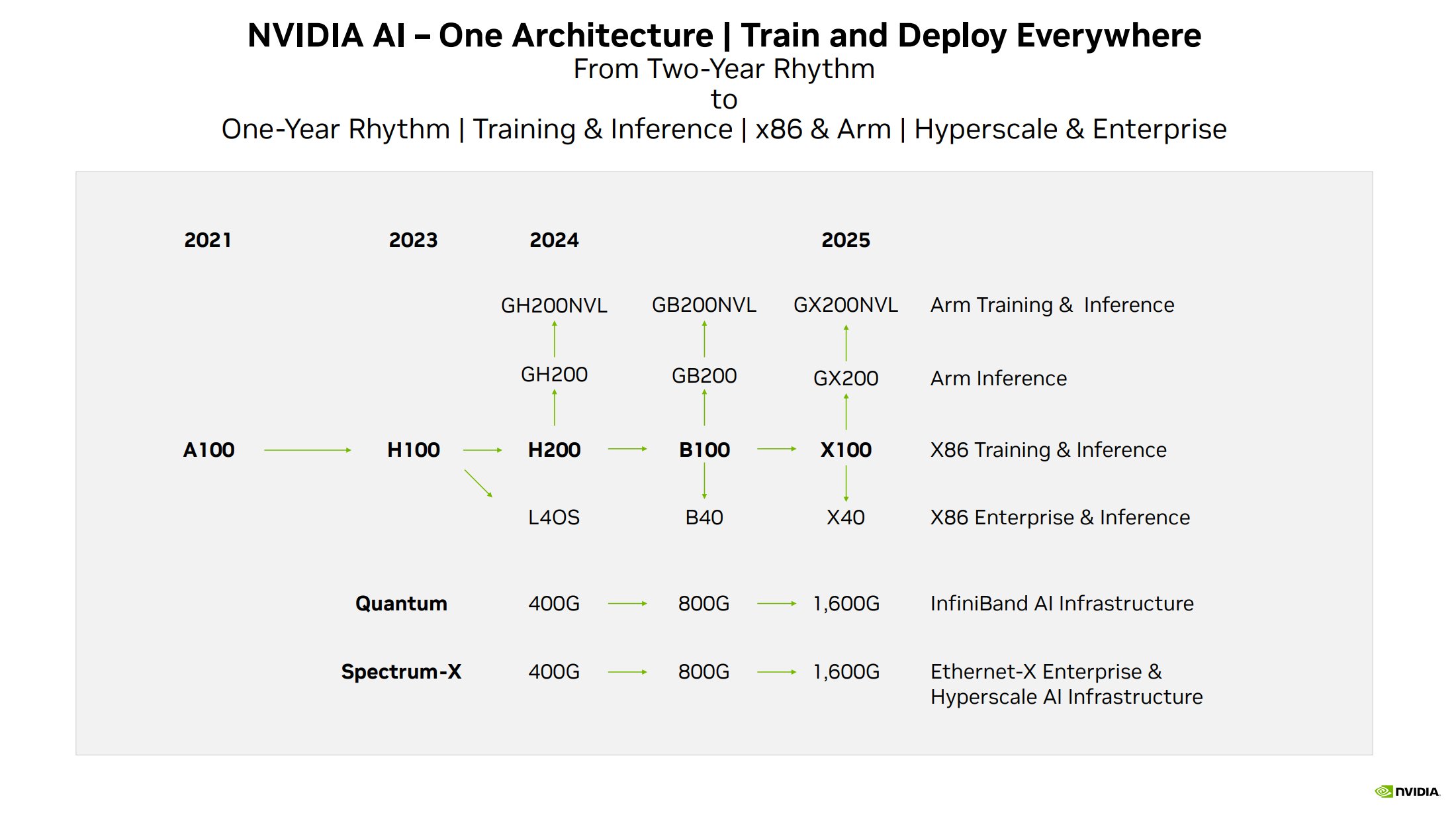
在过去的一段时间，内存的容量与带宽成为 NVIDIA 和 AMD 等硬件厂商们重点发力的方向。除了在硬件上堆料提升内存的带宽和容量，还有类似于 GH200 将通过 NVLink-C2C 将 CPU 与 GPU 互联起来，提供统一缓存一致性的内存空间的方案。算法和模型的进一步迭代，将会引领硬件的演进到什么方向呢？

ChatGPT 和 AlexNet 是一个量级的算法里程碑，AlexNet 拉开了上一个十年对算力的军备竞赛，ChatGPT 也是为未来十年芯片军备竞赛奠定了基调。正如我在前一阵提到的那样，内存和带宽会成为全新的需求，这件事如果只是单单大模型的需求，确定性还没那么高，但随着 NVidia、AMD 和 Intel 今年在内存和带宽上的发力会变得确定性更高。硬件的对内存和带宽的升级改造会进一步强化模型在内存和带宽上的扩展，而 ChatGPT 又给这方面的扩展对模型能力能达到的高度带来的足够确定性。 算法、硬件与钞票的微妙化学反应会不断强化这个逻辑，任何一方都没法控制这个走向。³³

最近一段时间，有一些人过早的离开了我们，怀念他们给我们带来的欢乐、知识与力量